נוסחאות יסודיות באופטיקה של עדשה

בפוסט כאן למדנו על הקשר בין העקמומיות של פני השטח של עדשה לבין היכולת שלה למקד את קרני האור. הפרמטרים שקובעים את יכולת המיקוד של העדשה, הם:

1. מקדם השבירה של החומר שממנו עשויה העדשה \(n\).
2. עובי העדשה \(d\).
3. רדיוס העקמומיות \(R\) של כל אחד מהצדדים שלה.

שלושת הפרמטרים הנ"ל קובעים את מרחק המוקד \(f\) של העדשה, שזה המרחק מהעדשה שאליו מתכנסות קרניים מקבילות שפוגעות בעדשה. כל הפרמטרים הנ"ל מוצגים בתרשים להלן:

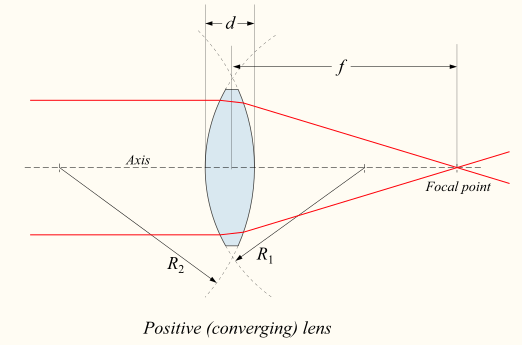
הנוסחה שמקשרת בין מרחק המוקד לשאר הפרמטרים היא:¹

\(\displaystyle \frac{1}{f}=(n-1)\left[ {\frac{1}{{{{R}_{1}}}}+\frac{1}{{{{R}_{2}}}}-\frac{{(n-1)d}}{{n{{R}_{1}}{{R}_{2}}}}} \right]\)

במידה והעדשה דקה מאוד, ניתן להניח כי \({d=0}\), ולכן נקבל:

\(\displaystyle \frac{1}{f}\approx \left( {n-1} \right)\left[ {\frac{1}{{{{R}_{1}}}}+\frac{1}{{{{R}_{2}}}}} \right]\)

העוצמה האופטית של עדשה \(P\) הופכית למרחק המוקד \(f\), וכן העקמומיות \(q\) של משטח הופכית לרדיוס-העקמומיות \(R\) של המשטח, ולכן את הנוסחה לעיל ניתן להציג גם באופן הבא:

\(\displaystyle P=\left( {n-1} \right)\left[ {{{q}_{1}}+{{q}_{2}}} \right]\)

מכאן ניתן לראות כי ככל שפני העדשה עקמומיים יותר, כך העוצמה האופטית שלה גדלה, והיא מסוגלת למקד את קרני האור בצורה חזקה יותר. זו הסיבה מדוע אנו מסוגלים להתמקד על עצמים רחוקים וקרובים גם יחד, כי שרירי העין שלנו מסוגלים לשנות את העקמומיות של עדשת העין ועל ידי כך לשנות את העוצמה האופטית שלה.

נוסחה נוספת הרלוונטית לעדשת העין שלנו, היא הנוסחה המקשרת בין מרחק האובייקט מהעין \({S}_{1}\), לבין המרחק בין העדשה ובין הדמות שנוצרת בתוך העין, מאחורי העדשה \({S}_{2}\). הנוסחה מקשרת בין גדלים אלה לבין העוצמה האופטית של העדשה \(P\):

\(\displaystyle P=\frac{1}{f}=\frac{1}{{{{S}_{1}}}}+\frac{1}{{{{S}_{2}}}}\)

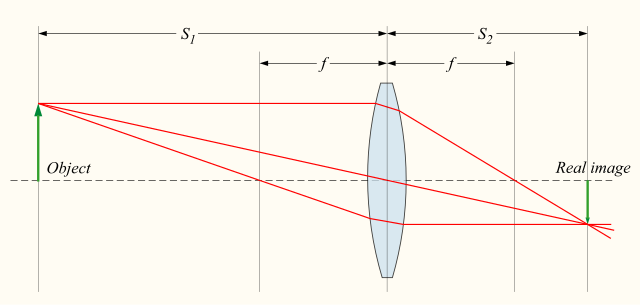
כדי לראות ברור ולא מטושטש, נדרוש כי הדמות תיווצר תמיד על הרשתית, ולכן \({S}_{2}\) צריך להיות מרחק קבוע. מכאן ניתן בקלות לראות כי ככל \({S}_{1}\) קטן יותר – כלומר האובייקט קרוב יותר לעין – כך העוצמה האופטית של העדשה \(P\) צריכה לגדול בהתאם, כדי שמיקום הדמות \({S}_{2}\) יהיה קבוע ותמיד על הרשתית.

מהתמונה למעלה ניתן לראות כי ניתן לקשר בין גובה האובייקט והדמות לבין המרחקים שלהם מהעדשה. קל לראות כי היחס בין גובה האובייקט \({H}_{o}\) (החץ הירוק בצד שמאל) ובין מרחק האובייקט \({S}_{1}\) שווה ליחס בין גובה הדמות \({H}_{i}\) (החץ הירוק מצד ימין) ובין מרחק הדמות \({S}_{2}\) (אלו שני ניצבים במשולשים ישרי זווית דומים). ולכן נקבל:

\(\displaystyle \frac{{{{H}_{i}}}}{{{{S}_{2}}}}=\frac{{{{H}_{o}}}}{{{{S}_{1}}}}\)

ההגדלה \(M\) היא למעשה היחס בין גובה הדמות לבין גובה האובייקט,² ולכן:

\(\displaystyle M=\frac{{{{H}_{i}}}}{{{{H}_{o}}}}=\frac{{{{S}_{2}}}}{{{{S}_{1}}}}\)

1. הסימן של רדיוס העקמומיות נבחר כך שעבור עדשה קמורה משני צדדיה – כלומר שפני העדשה בולטים כלפי חוץ – נקבל שרדיוס העקמומיות חיובי בשני צדדי העדשה. [↩]
2. לא התייחסתי כאן להגדלה חיובית או שלילית. במקרה הזה מדובר בהגדלה שלילית כי הדמות הפוכה, ולכן הגובה שלה מקבל סימן שלילי. [↩]