משפט נֵתֶר: המשפט היפה ביותר בפיזיקה

אֵמִּי נֵתֶר (1882-1935) נולדה בגרמניה למשפחה ממוצא יהודי. בתחילת דרכה, אמי הוכשרה ללמד צרפתית ואנגלית בבתי ספר לבנות, אך לבסוף החליטה ללמוד מתמטיקה באוניברסיטת ארלינגן, בה אביה – מקס נתר – היה פרופסור למתמטיקה.

זו הייתה החלטה מאוד לא שגרתית מצידה, כי האקדמיה באותה תקופה הייתה גברית לחלוטין. נשים כמעט ולא רכשו השכלה גבוהה, בוודאי שלא במדעים, וכצפוי אמי הייתה אחת משתי הסטודנטיות היחידות בכל האוניברסיטה. על משרות אקדמיות אין בכלל מה לדבר, כולן היו מאוישות בידי גברים. במשך כל תקופת לימודיה, אמי הייתה צריכה לקבל אישור מיוחד מכל מרצה כדי להיכנס לקורס שאותו לימד, ובכל מקרה הורשתה רק לצפות ולשמוע, אך לא לשאול שאלות או להשתתף באופן פעיל.

לאחר סיום לימודיה, ולאור הכישרון שהפגינה, המשיכה לעבוד באוניברסיטה, אך נאלצה לעבוד ללא שכר. באותה תקופה, אמי אפילו הנחתה בפועל סטודנטים לדוקטורט במתמטיקה, אך מבחינה רשמית הם לא היו רשומים תחתיה, אלא תחת שמו של אביה.

למרות כל המכשולים שבהם נתקלה, הכישרון שהפגינה לא נעלם מעיניו של דֵּוִיד הִילְבֵּרְט, גדול המתמטיקאים של התקופה, והוא הזמין אותה להיות חלק מהמחלקה למתמטיקה באוניברסיטת גטינגן. כצפוי, המהלך נתקל בהתנגדות משאר חברי האקדמיה, אך הפעם הילברט הוא זה שעמד לצידה של אמי, ובלתי אפשרי היה להתעלם מדרישותיו. אף על פי כן, למשך תקופה מסוימת היא עדיין נאלצה לעבוד ללא שכר גם באוניברסיטת גטינגן, ואף להרצות ולפרסם את מחקריה שלה תחת שמו של הילברט, כאשר היחס אליה היה רק בגדר "עוזרת מחקר", זו שכביכול מנגישה את רעיונותיו של הילברט הגדול.

שם באוניברסיטת גטינגן, אמי פרסמה את המשפט המתמטי המדהים שלימים נקרא בפשטות: משפט נתר. מי שהציג אותו לראשונה לאגודה המלכותית למדעים היה המתמטיקאי פֵלִיקְס קְלַיְין – ולא אמי בעצמה – שהרי כצפוי, אמי לא הייתה חברה באגודה.

אמי לבסוף גורשה מהאקדמיה בגרמניה בשנת 1933 בעקבות חוקי הגזע הנאצים, וברחה לארה"ב. לאחר מותה בשנת 1935, שלח אלברט איינשטיין מאמר הספד לניו-יורק טיימס, ובו כתב:

על פי אמות המידה של המתמטיקאים המוכשרים ביותר בימינו, אמי נתר היא הגאון המתמטי היצירתי והמשמעותי ביותר שזכינו לו עד כה, מאז החלו נשים לרכוש השכלה גבוהה.

אז מהו משפט נתר המפורסם ואלו תובנות הוא חושף?

יש לשמור על החוקים

בחלק הראשון של המאמר, אתמקד בתיאור פופולרי של משפט נתר כדי להמחיש את הרעיון הכללי שעומד בבסיס של כל העסק. את הדיון הטכני אשמור לחלק השני, למי מכם שמעוניין בכך.

במילים פשוטות, משפט נתר טוען את הטענה הבאה:

לכל סימטריה שנוכל למצוא בחוקי הפיזיקה, קיים חוק שימור המייצג גודל שאינו משתנה עם התפתחות המערכת הפיזיקלית.

אוקיי, בואו ננסה להתמודד עם המשפט הזה צעד צעד. בשלב הראשון, יש להבין מהו חוק שימור. הדרך הטובה ביותר להבין זאת היא באמצעות דוגמה מחיי היומיום, למשל: ירי באקדח. כולנו יודעים כי כאשר כדור נפלט מאקדח, נוצר רֶתַע והאקדח עצמו נע אחורה. הסיבה לרתע של האקדח, היא חוק שימור שאחראי לכך שגודל פיזיקלי מסויים נשמר ואינו משתנה במהלך הירי. במקרה זה, הגודל הנשמר במערכת נקרא: תנע קווי.

התנע של גוף שווה למכפלת מסת הגוף במהירות שלו, ובמקרה שלנו, התנע של המערכת כולה נשמר (מערכת = אקדח + כדור). אם התנע הכולל היה \({0}\) לפני הירי (כי האקדח עם הכדור נמצאים במנוחה ללא מהירות) הוא צריך להיות \({0}\) גם לאחר הירי. לאחר הירי הכדור קיבל תנע (כי יש לו מהירות), ולכן גם האקדח צריך לקבל תנע, אך בכיוון הנגדי (מכאן הרתע של האקדח). לכן סה"כ, התנע הכולל של המערכת נשאר \({0}\) גם לאחר הירי.

פיזיקאים קוראים לתופעה זו: חוק שימור תנע קווי.¹

דוגמה פשוטה נוספת היא מתנועת הלוך ושוב של נדנדה בגן משחקים. בכל רגע נתון יש לנדנדה אנרגיה קינטית (עקב מהירות הנדנדה), ואנרגיה פוטנציאלית (עקב הגובה של הנדנדה מהקרקע). במערכת זו, הגודל הנשמר הוא האנרגיה הכוללת של הנדנדה, כלומר: האנרגיה הקינטית והפוטנציאלית גם יחד.

כל אימת שהנדנדה מגיעה לשיא הגובה, היא צוברת מקסימום אנרגיה פוטנציאלית, אך \({0}\) אנרגיה קינטית (כי היא עוצרת לרגע). הנדנדה מיד חוזרת לנקודת האמצע וממירה את כל האנרגיה הפוטנציאלית שצברה בשיא הגובה לאנרגיה קינטית (לכן מהירות הנדנדה מקסימלית בנקודת האמצע). במהלך תנועת הנדנדה, האנרגיה הקינטית מתחלפת לפוטנציאלית ולהיפך, שוב ושוב, אך בכל רגע נתון סך האנרגיה נשמר. פיזיקאים קוראים לתופעה זו: חוק שימור אנרגיה.

ישנו חוק שימור נוסף מפורסם הנקרא: שימור תנע זוויתי. במקרה זה לא אכנס יותר מדי לפרטים טכניים, כי הרעיון הכללי של חוק שימור כבר לבטח מובן משתי הדוגמאות הקודמות. רק אדגיש כי כמו אנרגיה ותנע קווי, ישנו גם גודל נוסף הנקרא תנע זוויתי, וגם הוא נשמר במערכת. דוגמה פשוטה לכך ניתן לראות בהחלקה אומנותית על הקרח, כאשר המחליק מסתובב סביב עצמו ומסוגל להגביר את מהירות הסיבוב שלו באמצעות קירוב הידיים והרגליים אל מרכז הגוף. בגלל שהתנע הזוויתי של המחליק נשמר, מהירות הסיבוב שלו הולכת וגדלה ככל שמסתו מרוכזת קרוב יותר לציר הסיבוב. ניתן לראות זאת באנימציה הבאה:

אוקיי, אז לסיכום, למדנו על שלושה חוקי שימור:

1. חוק שימור אנרגיה,
2. חוק שימור תנע קווי,
3. חוק שימור תנע זוויתי.

אלא שלאחר כל התאור הנ"ל, נשארה שאלה אחת חשובה ובסיסית:

למה קיימים מלכתחילה חוקי שימור?

חשבו על כך: למה אנרגיה כוללת צריכה בכלל להישמר? למה תנע קווי צריך להישמר? זו שאלה שמופנית ישירות אל הטבע שבו אנו חיים; במילים אחרות: מדוע כך הם פני הדברים? למה יש ביקום שלנו חוקי שימור? מהו אותו גורם שבפועל "דואג" לשמר את האנרגיה, את התנע הקווי והתנע הזוויתי? מי "אחראי" לכך?

בנקודה זו בדיוק נכנסת לתמונה אמי נתר, עם תשובה גאונית ומבריקה. נתר הוכיחה מתמטית כי כל חוק שימור נובע ישירות מתוך סימטריה שקיימת בתוך חוקי הפיזיקה עצמם (ותיכף אסביר למה הכוונה במילה: סימטריה).

אמי נתר הגיעה למסקנה כי אם נוכל למצוא סימטריה מסוג מסוים בחוקי הפיזיקה, אותה סימטריה היא זו שאחראית לכך כי קיים גודל פיזיקלי כלשהוא שנשמר במערכת. אם נמצא סימטריה נוספת מסוג אחר, סימטריה זו תהיה אחראית לגודל פיזיקלי אחר שנשמר במערכת. בקיצור: לכל סימטריה שנוכל למצוא בחוקי הפיזיקה, ניתן לשייך גודל פיזיקלי מתאים שנשמר במערכת. לכן באופן כללי ניתן לומר כי:

סימטריות יוצרות חוקי שימור.

זו טענה יפה ועמוקה בצורה יוצאת מגדר הרגיל, כי היא קושרת בין חוקי טבע (או: חוקי שימור) לבין תכונות יסודיות של הטבע עצמו (או: סימטריות).

אם נחזור לרגע לחוקי השימור שהצגתי קודם לכן, משפט נתר קובע כי: 1. חוק שימור האנרגיה נובע מכך שלפיזיקה יש סימטריה להזזה בזמן, 2. חוק שימור התנע הקווי נובע מכך שלפיזיקה יש סימטריה להזזה במרחב, 3. וחוק שימור התנע הזוויתי נובע מסימטריה לסיבוב במרחב.

למה הכוונה?

סימטריה זמנית <=> שימור אנרגיה

לחוקי הפיזיקה לא אכפת מתי הם פועלים; הפיזיקה של אתמול זהה לפיזיקה של היום, ושני אלו זהים לפיזיקה של מחר. המשפט האחרון אולי נשמע לכם טריוויאלי, אך מבחינה מתמטית מדובר בסימטריה, כלומר: ניתן להזיז את משתנה הזמן קדימה ואחורה (אל העבר והעתיד) וחוקי הפיזיקה לא ישתנו. הסימטריה בזמן שיש לחוקי הפיזיקה מתבטאת בכך שחוקי הטבע ביקום שבו אנו חיים נשארים זהים בזמנים שונים.

אמי נתר הוכיחה מתמטית כי הסימטריה הספציפית הזו – הסימטריה בזמן – היא זו שאחראית לחוק שימור האנרגיה! מי שדואג לכך שהאנרגיה הכוללת תישמר בכל רגע רגע, זו הסימטריה הזמנית שמובנית בטבע! יש כאן טענה מדהימה ומהפכנית, ונוכל לנסח אותה גם הפוך:

אם חוק שימור האנרגיה לא היה מתקיים, פירוש הדבר היה שאנו חיים ביקום שבו הפיזיקה של היום זו אינה הפיזיקה של הלילה.

סימטריה מרחבית <=> שימור תנע קווי

כל האמור לעיל נכון גם לגבי חוק שימור התנע הקווי. לפי משפט נתר, אם קיים חוק שימור תנע קווי, משמע יש סימטריה כלשהיא שיוצרת אותו (ולהיפך). במקרה של שימור תנע קווי, מדובר בסימטריה מרחבית.

לחוקי הפיזיקה לא אכפת היכן הם פועלים; הפיזיקה של כאן זהה לפיזיקה של שם, ושני אלו זהים לפיזיקה של כל מקום אחר. שוב, גם המשפט הנ"ל אולי נראה לכם טריוויאלי, אך מבחינה מתמטית מדובר בסימטריה, כלומר: ניתן להזיז את משתנה המיקום קדימה ואחורה (אל מקום רחוק או קרוב) וחוקי הפיזיקה לא ישתנו. הסימטריה במרחב שיש לחוקי הפיזיקה מתבטאת בכך שחוקי הטבע ביקום שבו אנו חיים נשארים זהים במקומות שונים.

הסימטריה הספציפית הזו – הסימטריה במרחב – היא זו שאחראית לחוק שימור התנע הקווי! מי שדואג לכך שהתנע הקווי נשמר בכל רגע רגע, זו הסימטריה המרחבית שמובנית בטבע. גם זו טענה מדהימה ומהפכנית, וגם אותה נוכל לנסח באופן הפוך:

אם חוק שימור התנע הקווי לא היה מתקיים, פירוש הדבר היה שאנו חיים ביקום שבו הפיזיקה של כאן זו אינה הפיזיקה של שם.

סימטריה סיבובית <=> שימור תנע זוויתי

חוק שימור התנע הזוויתי, גם הוא נובע מתוך סימטריה הנקראת: סימטריה סיבובית. במילים פשוטות: לחוקי הפיזיקה לא אכפת מאיזה כיוון מסתכלים עליהם; אם תסובבו את כל גלקסיית שביל החלב בכל זווית או כיוון שתרצו, תגלו כי מבחינת חוקי הפיזיקה, שום דבר מהותי לא השתנה ולמַנַּח המדויק של הגלקסיה או לאוריינטציה שלה במרחב אין משמעות מבחינת חוקי הפיזיקה.

באופן דומה ניתן לומר כי:

אם חוק שימור התנע הזוויתי לא היה מתקיים, פירוש הדבר היה שאנו חיים ביקום שבו הפיזיקה של מבט מצד אחד אינה הפיזיקה של מבט מצד אחר.

סיכום

ראינו כי משפט נתר חושף את הקשר בין סימטריות לבין חוקי שימור. נוכל לסכם את כל מה שלמדנו באופן הבא:

1. שימור אנרגיה כללית הוא תוצאה של העובדה כי חוקי הפיזיקה זהים בכל נקודה בזמן, כך שהרגע שבו מערכת פיזיקלית קיימת אינו משחק תפקיד; המערכת נשלטת על ידי חוקי פיזיקה זהים גם בזמנים שונים.
2. שימור תנע קווי הוא תוצאה של העובדה כי חוקי הפיזיקה זהים בכל נקודה במרחב, כך שהמקום שבו מערכת פיזיקלית קיימת אינו משחק תפקיד; המערכת נשלטת על ידי חוקי פיזיקה זהים גם במקומות שונים.
3. שימור תנע זוויתי הוא תוצאה של העובדה כי חוקי הפיזיקה זהים בכל כיוון, כך שהאוריינטציה שבה מערכת פיזיקלית נמצאת במרחב אינה משחק תפקיד; המערכת נשלטת על ידי חוקי פיזיקה זהים גם במַנַּחים שונים.

מדהים, לא ככה?

נספח טכני (למיטיבי לכת)

כל האמור לעיל הוא תיאור פופולרי של משפט נתר, למרות שהוא מספיק כדי להבין את עיקר הרעיון שעומד מאחורי המשפט. מבחינה טכנית, יש מספר דקויות שצריך לשים אליהן לב, ועל כך אני רוצה להרחיב כעת.

משפט נתר הוא משפט שמתמקד בפונקציה שפיזיקאים מאוד אוהבים שנקראת: פונקציית לגראנז', על שם המתמטיקאי ז'וזף-לואי לגראנז' (1736-1813). בהמשך אציג לכם כיצד נראית פונקציית לגראנז' עבור מספר מערכות פשוטות, אך בשלב זה רק אציין כי פונקציית לגראנז' מסומנת באות \(L\), ופיזיקאים מאוד אוהבים לתאר מערכות פיזיקליות באמצעות פונקציה זו.

במקרה הכללי הפונקציה תהיה תלויה במשתנים של המערכת, כגון: משתנה הזמן \(t\), המיקום \(x\), והמהירות \(v\), כך:

\(L\left( {t,x,v} \right)\)

הסיבה שאנו מתארים מערכת פיזיקלית באמצעות פונקציית לגראנז' \(L\), היא כי את משוואות התנועה של המערכת – כלומר: המשוואות שקובעות כיצד המערכת תתפתח לאורך זמן – ניתן לגזור ישירות מתוך הפונקציה \(L\), ועל ידי כך לקבל תיאור מתמטי מלא של המערכת. להלן אציג בפניכם את משוואת התנועה של המערכת, אך רק באופן ויזואלי ומבלי להיכנס לפרטים, כי זו אינה המטרה. מה שחשוב הוא רק שתשימו לב כיצד המשוואה מבוססת כולה על פונקציית לגראנז' \(L\), ואם הפונקציה ידועה לנו, ניתן בקלות לגזור מתוכה את משוואת התנועה של המערכת:²

\(\displaystyle \frac{d}{{dt}}\left( {\frac{{\partial L}}{{\partial v}}} \right)=\frac{{\partial L}}{{\partial x}}\)

משפט נתר קובע כי לפונקציה \(L\) יש סימטריה רציפה, אם נוכל לעשות טרנספורמציה לאחת מהקואורדינטות של הפונקציה \(L\), אך למרות הטרנספורמציה משוואות התנועה של המערכת לא ישתנו.³ משפט נתר מבטיח כי כל אימת שנמצא טרנספורמציה שכזו, משמע מצאנו סימטריה רציפה שתגרור אחריה חוק שימור שמיוחד אך ורק לה.

להלן מספר דוגמאות פשוטות להמחשת העיקרון. נסתכל לדוגמה על מערכת המורכבת מגוף המחובר לקפיץ ומתנדנד הלוך ושוב בתנועה מחזורית:

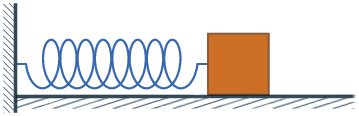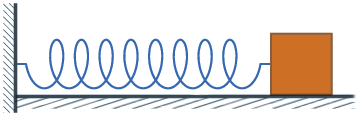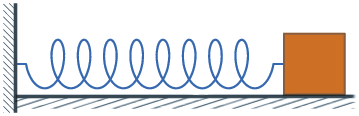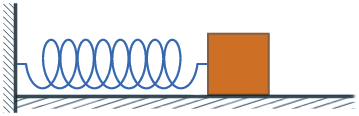
כך נראית פונקציית לגראנז' של המערכת הנ"ל:

\(\displaystyle L=\frac{m}{2}{{v}^{2}}-\frac{k}{2}{{x}^{2}}\)

כאשר \(m\) זו מסת הגוף, \(v\) זו המהירות, \(x\) זה המיקום, ו- \(k\) זה קבוע המציין את עוצמת הקפיץ.

עכשיו חשבו לרגע האם במערכת זו קיימת סימטריה מרחבית? במילים אחרות: מה יקרה אם נבצע טרנספורמציה לקואורדינטה \(x\) של מיקום הגוף, למשל: אם נזיז את הגוף במרחב ימינה או שמאלה, מנקודה אחת לנקודה אחרת? ברור כי הקפיץ ימתח או יתכווץ, מה שיגרום לשבירת הסימטריה במערכת. לפי משפט נתר, אם אין סימטריה מרחבית לא נקבל את חוק שימור התנע הקווי, ובאמת התנע הקווי של הגוף לא נשמר. להזכירכם, התנע של הגוף הוא מכפלת מסתו במהירות שלו (כלומר: \(p=m\cdot v\)), ותחת השפעת הקפיץ מהירות הגוף \(v\) משתנה כל הזמן, כלומר: אין שימור תנע קווי.

אבל! שימו לב כי הפונקציה \(L\) אמנם תלויה במיקום \(x\) ובמהירות \(v\), אך היא אינה תלויה בזמן \(t\) ! משתנה הזמן \(t\) פשוט אינו מופיע בפונקציה \(L\), ולכן טרנספורמציה לקואורדינטת הזמן לא תשנה את הפונקציה \(L\) וממילא גם משוואות התנועה של המערכת – שנגזרות מתוך הפונקציה \(L\) – לא ישתנו.⁴

במילים אחרות: גילינו סימטריה בזמן. לפי משפט נתר, אם קיימת סימטריה היא בהכרח גוררת אחריה חוק שימור, ובמקרה של סימטריה בזמן, נתר הוכיחה מתמטית כי הגודל הנשמר במערכת הוא האנרגיה הכוללת: בכל רגע נתון יש לגוף אנרגיה קינטית (עקב המהירות שלו), ואנרגיה פוטנציאלית (עקב המתיחה והכיווץ של הקפיץ). כל אימת שהקפיץ נמתח או מתכווץ הגוף צובר אנרגיה פוטנציאלית, אך בו-זמנית מאבד אנרגיה קינטית. האנרגיה הקינטית מתחלפת לפוטנציאלית ולהיפך, שוב ושוב, אך בכל רגע נתון סך האנרגיה – הקינטית והפוטנציאלית יחד – נשמר.⁵

אוקיי, אז מצאנו סימטריה בזמן אך לא במרחב. אבל מה יקרה אם נניח כי ברגע מסוים הקפיץ נקרע, והגוף השתחרר מהשפעת הקפיץ? כעת אין קפיץ בכלל ולכן \({k=0}\), ופונקציית לגראנז' תראה כך:

\(\displaystyle L=\frac{m}{2}{{v}^{2}}\)

כעת דווקא כן קיימת סימטריה מרחבית במערכת, כי הפונקציה \(L\) אינה תלויה יותר במיקום הגוף \(x\), לכן טרנספורמציה של קואורדינטת המיקום לא משנה שום דבר מהותי. ברגע שבו הגוף חופשי מהשפעת הקפיץ, נוצרה במערכת סימטריה מרחבית, והיא גוררת אחריה את חוק שימור התנע הקווי. במצב שכזה באמת נגלה כי הגוף ימשיך לנוע באותה מהירות \(v\) שבה הוא נע ברגע הניתוק מהקפיץ, ומרגע הניתוק והלאה, התנע הקווי שלו נשמר.⁶

באופן דומה נוכל לדמיין מערכת המורכבת משני גופים המחוברים ביניהם בקפיץ אחד משותף. גם במערכת זו קל לנחש כי הזזה מרחבית של קואורדינטת המיקום של כל גוף בנפרד תמתח או תכווץ את הקפיץ ולכן תשבור סימטריה. מכאן נובע כי התנע הקווי של כל גוף בנפרד לא ישמר. אך אם נזיז במרחב את שני הגופים יחד – בדיוק באותה מידה – לא נשבור את הסימטריה. לפי משפט נתר, סימטריה מרחבית גוררת אחריה חוק שימור תנע קווי, ובמקרה הזה אכן מדובר בשימור התנע הקווי של שני הגופים יחד. אע"פ שהתנע הקווי של כל גוף בנפרד משתנה בכל רגע, עדיין התנע של שניהם יחד נשמר בכל רגע.⁷

סימטריה סיבובית – זו הגוררת אחריה את חוק שימור התנע הזוויתי, ניתן להדגים באמצעות מערכת דו-ממדית (בניגוד לגוף המחובר לקפיץ שם התנועה היא במימד אחד בלבד). בתור מערכת דו-ממדית ניקח לדוגמה את המסלול של לווין המקיף את כדור הארץ:

פונקציית לגראנז' של הלווין נראית כך:

\(\displaystyle L=\frac{m}{2}{{v}^{2}}+\frac{{GMm}}{r}\)

ניתן לראות כי אין לפונקציה \(L\) תלות בזמן, לכן קיימת סימטריה בזמן ונצפה כי האנרגיה הכוללת של הלווין תישמר. לעומת זאת, אין סימטריה מרחבית, כי שינוי המרחק מכדור הארץ \(r\) יגרור שינוי בעוצמת כוח הכבידה (בדומה לשינוי כוח הקפיץ בדוגמה הקודמת), ולכן נצפה שהתנע הקווי של הלווין לא ישמר.⁸

אבל! אע"פ שפונקציה \(L\) תלויה בקואורדינטה \(r\) שהיא המרחק לכדור הארץ, שימו לב ש- \(L\) אינה תלויה במיקום הזוויתי של הלווין ביחס לכדור הארץ. כל מה שמשפיע על פונקציה \(L\) זה המרחק של הלווין לכדור הארץ ולא המיקום המדויק של הלווין לאורך המסלול. בניגוד לשינוי של קואורדינטה \(r\), שינוי המיקום הזוויתי של הלווין אינו משנה את עוצמת כוח הכבידה של כדור הארץ. במילים אחרות: לשדה הכבידה של כדור הארץ יש סימטריה סיבובית, כי עוצמתו תלויה אך ורק במרחק לכדור הארץ. זאת אומרת שמצאנו במערכת סימטריה סיבובית, ולכן נצפה שיהיה גודל נוסף שנשמר במערכת, וגודל זה הוא התנע הזוויתי של הלווין.⁹

1. קל להבין מדוע מהירות האקדח קטנה ביחס לכדור; הרי לאחר הירי, האקדח מקבל את התנע של הכדור הנפלט, אך בכיוון הנגדי. אמנם מהירות הכדור גבוהה, אך מסת הכדור קטנה. מכאן נובע כי אם מסת האקדח גדולה, אז מהירות הרתע שלו תהיה קטנה. [↩]
2. אם אתם חדי העין תוכלו להבחין כי משוואה זו היא למעשה החוק השני של ניוטון בתחפושת. על פי החוק השני של ניוטון, הכוח שווה לנגזרת בזמן של התנע. באגף ימין של המשוואה ניתן לראות כי אנו מחלקים את פונקציית לגראנז' במיקום. לפונקציה L יש יחידות של אנרגיה, ובמכניקה ניוטונית העבודה (שהיא אנרגיה) היא למעשה מכפלת הכוח בהעתק, לכן מחלוקת L במיקום נקבל כוח. באגף השמאלי תוכלו לראות שאנו מחלקים את L במהירות. כידוע, האנרגיה היא למעשה מסת הגוף כפול המהירות בריבוע, לכן אם נחלק אנרגיה במהירות נקבל יחידות של מסה כפול מהירות, כלומר: תנע. אם נגזור גודל זה בזמן נקבל את החוק השני של ניוטון. [↩]
3. משפט נתר דורש סימטריה רציפה במובן זה שטרנספורמציה לקואורדינטות ניתן להפעיל באופן אינפיניטסימלי, כלומר: קטן ככל שנרצה. למשל: למשולש שווה צלעות אין סימטריה סיבובית רציפה, כי נצטרך לסובב את המשולש בקפיצות של 120 מעלות כדי שהמשולש יחזור למצב המקורי שלו. לתבנית שתי וערב (כמו דף משבצות חשבון) אין סימטריה מרחבית רציפה כי נצטרך להזיז את התבנית ביחידות בדידות בלבד כדי שהתבנית תחזור למצב המקורי שלה. [↩]
4. במקרה הזה משתנה הזמן אינו מופיע באופן מפורש בפונקציה L, אך הוא מופיע באופן בלתי מפורש, כי גם המיקום והמהירות תלויים בזמן. אלא שמשפט נתר קובע כי מספיק שמשתנה הזמן לא יופיע באופן מפורש כדי לקיים את חוק שימור האנרגיה. [↩]
5. באופן כללי ניתן לומר כי האנרגיה של מערכת נשמרת במידה והיא מבודדת מכוחות שאינם משמרים, לדוגמה: כוח חיכוך. במקרה של הגוף המחובר לקפיץ, אם בין הגוף לבין המשטח שתחתיו היה פועל כוח חיכוך, שימור אנרגיה לא היה מתקיים. [↩]
6. יש להדגיש כי סימטריה בפונקציה L לא חייבת להתקבל רק במידה וקואורדינטה מסוימת חסרה. גם אם קואורדינטה מסוימת מופיעה בפונקציה L, עדיין יש טרנספורמציות שניתן להפעיל על הקואורדינטה שלא ישנו את משוואות התנועה של המערכת. [↩]
7. באופן כללי ניתן לומר כי התנע הקווי של מערכת נשמר במידה והיא מבודדת מכוחות חיצוניים. [↩]
8. בתנועה מעגלית אמנם גודל המהירות נשאר קבוע אך כיוון המהירות משתנה, ולכן התנע הקווי לא נשמר. [↩]
9. באופן כללי ניתן לומר כי התנע הזוויתי של מערכת נשמר אע"פ שפועלים עליה כוחות חיצוניים, ובלבד שהכוחות החיצוניים לא מפעילים עליה מומנט-כוח. [↩]