מהי האקסיומה הראשונה של תורת היחסות? מה מלכתחילה הניע את איינשטיין לחשוב מחדש על העקרונות היסודיים ביותר של הפיזיקה? כל התשובות, בסדרה הבאה המוקדשת לתורת היחסות.
שנת 1905 נקראת על ידי פיזיקאים: "שנת הפלאות", והיא אכן הייתה שנה מופלאה!
בשנה זו – בהיותו בן 26 בלבד – פרסם אלברט איינשטיין ארבעה מאמרים ששינו את עולם הפיסיקה, ובישרו את תחילתה של הפיסיקה המודרנית שהתפתחה במהלך המאה העשרים:
- במאמר הראשון איינשטיין הציע הסבר לאפקט הפוטואלקטרי, אפקט שפיסיקאים לא הצליחו להסביר קודם לכן. האפקט הפוטואלקטרי שווה פוסט נפרד, לכן מבלי להיכנס כרגע לפרטים טכניים מדי, חשוב רק לדעת כי איינשטיין הצליח להסביר את האפקט הנ"ל באמצעות התובנה שהאנרגיה של קרינה אלקטרומגנטית מגיעה במנות בדידות, ולא רציפות. תובנה זו כבר נתגלתה בשנת 1900 ע"י הפיזיקאי הגרמני מַקְס פּלַנְק, אך איינשטיין השתמש בה כדי להסביר את האפקט הפוטואלקטרי. מעניין לציין כי איינשטיין קיבל בשנת 1921 את פרס הנובל על עבודה זו, ולא על תורת היחסות כפי שנהוג לחשוב.
- במאמר השני איינשטיין הציג מודל לתנועה הַבְּרָאוּנִית, שהיא התנועה האקראית של אטומים ומולקולות בחומר. עבודה זו נתנה חיזוק משמעותי לדעה התומכת בכך שהחומר אינו רציף, אלא בדיד, כלומר: מורכב מאטומים (באותה תקופה נושא זה עדיין היה נתון במחלוקת). הוויכוח הוכרע סופית לאחר שתחזיותיו של איינשטיין אומתו באופן ניסיוני בשנת 1908 על ידי הפיזיקאי הצרפתי זָ'אן-בָּטִיסְט פֵּרִין, שלימים קיבל את פרס הנובל על עבודתו בתחום.
- במאמר השלישי איינשטיין עוסק בתנועתם של גופים הנעים במהירות הקרובה למהירות האור. תורת היחסות הפרטית למעשה מבוססת על המאמר הנ"ל.
- במאמר הרביעי איינשטיין מציג את המשוואה המפורסמת: \({E=mc^2}\), משוואה המקשרת בין מסה לאנרגיה ומנבאת את הפוטנציאל האדיר הגלום באנרגיה גרעינית ובפצצת האטום. בשני הפוסטים האחרונים בבלוג עסקתי בהרחבה במשוואה הזו (ראו בקישור כאן, וכאן).
המטרה של סדרת הפוסטים שתבוא עלינו לטובה, היא להסביר בצורה פשוטה (ככל האפשר) את עקרונות הבסיס של תורת היחסות, מהן התופעות הפיזיקליות שתורה זו מנבאת, ובכלל מה גרם לאיינשטיין לנסות ולחשוב מחדש על עקרונות היסוד של הפיסיקה.
אוקיי, בואו נתחיל.
כולם צודקים
הזרעים הראשונים של תורת היחסות הוטמנו עוד במאה ה-17 ע"י הפיזיקאי האיטלקי המפורסם גלילאו גליליי, הרבה לפני איינשטיין. לאחר עשרות שנים של מחקר, ניסויים ותצפיות, גלילאו (כמעט בגיל 70) הגיע למסקנה הבאה:
חוקי המכניקה השולטים בתנועתם של גופים במרחב, זהים בכל מערכת ייחוס שנעה במהירות קבועה בקו ישר.
גלילאו בעצם טוען את הטענה הבאה: צופה הנמצא בתוך מערכת שנעה במהירות קבועה בקו ישר (מערכת שכזו נקראת: מערכת אינרציאלית), לא יוכל להסיק מהי מהירותו בפועל ע"י בחינה של תנועת גופים במרחב שסביבו.1
אם הניסוח הטכני הנ"ל לא ממש עוזר, אל דאגה! יש לי הסבר הרבה יותר פשוט:
נניח שאתם נמצאים בתוך רכבת נוסעת (זו ה- "מערכת"). כשאתם נמצאים בתוך הרכבת, אין לכם מושג אם אתם אכן דוהרים במהירות של 100 קמ"ש, או אולי אתם בכלל במנוחה על הקרקע, עוד לפני שהרכבת יצאה מהתחנה. אם בפועל אתם כן מצליחים להבדיל, אז זה רק בגלל רעש המנוע, הנוף מהחלון, טלטלה של הרכבת עקב המגע עם המסילה וכו'. אבל אם כל הסימנים האלה ינוטרלו לגמרי, אז לא יהיה לכם שום דרך לדעת האם הרכבת בתנועה, או במנוחה. הרכבת מבחינתכם תהיה כמו "קפסולה" אטומה, ולכם לא יהיה מושג מה מצב הרכבת ביחס לעולם שבחוץ, כלומר: האם הרכבת עומדת בתחנה או שמא כבר דוהרת ליעד.
גם אם תנסו להתחכם ולבצע איזה ניסוי בתוך הרכבת, ומתוך תוצאות הניסוי להסיק מה מצב הרכבת, אז צפויה לכם אכזבה… לדוגמה: אתם יכולים לשחק כדורסל, באולינג או ביליארד בתוך הרכבת, ותנועת הכדורים במרחב לא תהיה תלויה בשאלה האם הרכבת נמצאת בתנועה או במנוחה. מה ששולט בתנועתם של הכדורים (וכל דבר אחר), אלה חוקי המכניקה. לפי העיקרון של גלילאו, כל ניסוי שתבצעו בתוך הרכבת יציית לאותם חוקים בדיוק, ויראה לכם בדיוק אותו דבר גם אם הרכבת נעה במהירות של 10 קמ"ש, 100 קמ"ש או אפילו לא נעה בכלל (0 קמ"ש).
עיקרון זה נכון גם במקרה של שתי מערכות הנעות במהירות קבועה אחת ביחס לשניה. צופה מתוך המערכת (לא משנה איזה), לא יוכל לקבוע באופן מוחלט מי "באמת" נמצאת בתנועה ומי "באמת" נמצא במנוחה. הכל יחסי, ושני הצדדים צודקים.

מהעיקרון של גלילאו ניתן להגיע למסקנה מאוד חשובה, והיא: תנועה במרחב היא תמיד יחסית, ולא אבסולוטית. כל פעם שאנו מנסים למדוד תנועה, אנו צריכים לבחור מערכת ייחוס ואנו עושים זאת מטעמי נוחות בלבד: תנועת מכונית נמדדת ביחס למדרכה, תנועת לוויינים נמדדת ביחס למרכז כדור הארץ, ותנועת מרכז כדור הארץ נמדדת ביחס לשמש, אבל ברור לכם כי גם לוויינים וגם מרכז כדור הארץ וגם השמש כולם נעים גם ביחס למדרכה, אם ממש נתעקש…
כדי שנהיה מסוגלים למדוד תנועה באופן אבסולוטי ולא יחסי, צריך למצוא מערכת ייחוס אבסולוטית, ואין כזו. אם נתעקש ובכל זאת ננסה לבחור מערכת אבסולוטית שכזו, נגלה תמיד שהבחירה שלנו היא שרירותית לחלוטין. מישהו אחר, בזמן אחר ובמקום אחר, יכול לבחור מערכת ייחוס אחרת לגמרי, מסיבות אחרות.
כך עברו להם השנים, ובמהלכם ניסו למצוא סדקים בעיקרון הנ"ל של גלילאו, סדקים שאולי כן יאפשרו לנו למצוא מערכת ייחוס אבסולוטית, אך ללא הצלחה.
אלא שתקווה חדשה הופיעה במחצית השנייה של המאה ה-19, כאשר הפיזיקאי הסקוטי גֵ'יימְס קְלֵרְק מַקְסְוֶל ניסח את "משוואות מקסוול", ארבע משוואות דיפרנציאליות המתארות את הקשר בין מטענים חשמליים לבין השדות האלקטרומגנטיים שהם יוצרים מסביבם. אם המכניקה מגולמת בתוך חוקי ניוטון, אז האלקטרודינמיקה מגולמת במשוואות מקסוול.
על ידי הצלבת משוואות מקסוול זו בזו (ובתוספת קצת מתמטיקה), ניתן להראות כי קרינה אלקטרומגנטית – קרינה שאנו קוראים לה בפשטות: אור – מצייתת למשוואה מאוד ספציפית הנקראת: משוואת הגלים. מכאן נובע כי האור שסביבנו הוא למעשה גל, או בניסוח יותר טכני: האור אלו תנודות בשדה האלקטרומגנטי. האור הנ"ל (שהוא כאמור גל), מתקדם במרחב במהירות של כ- 300,000 ק"מ בשניה, מהירות הנקראת בפשטות: מהירות האור.
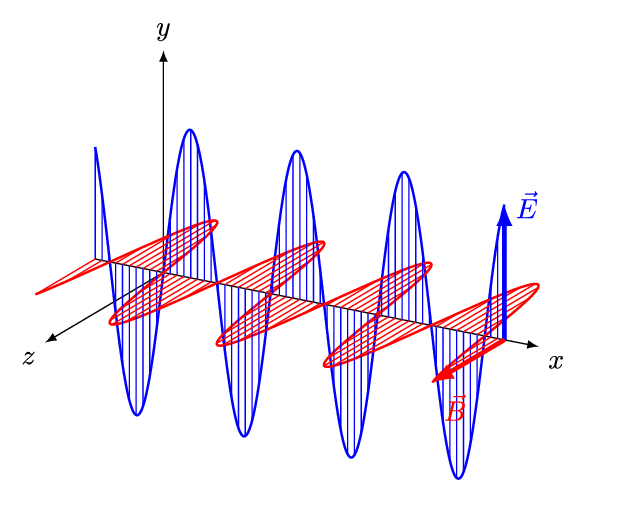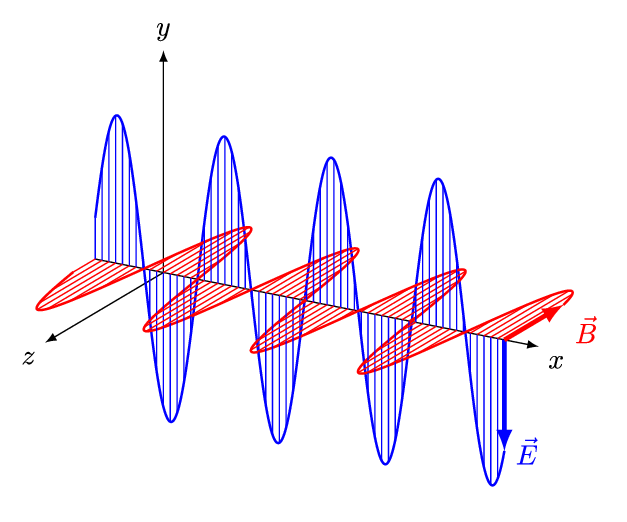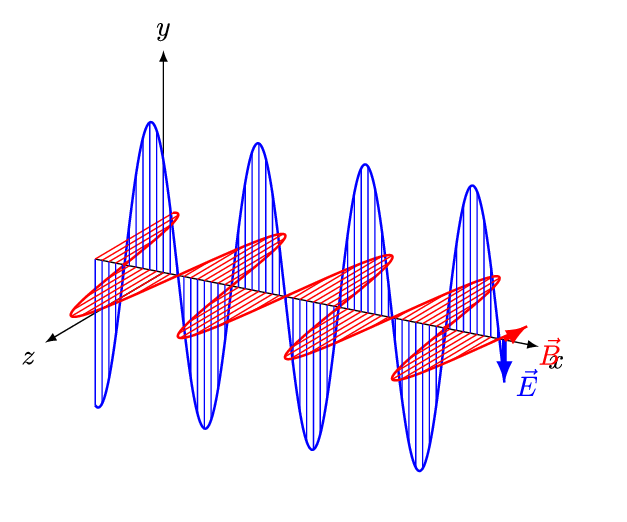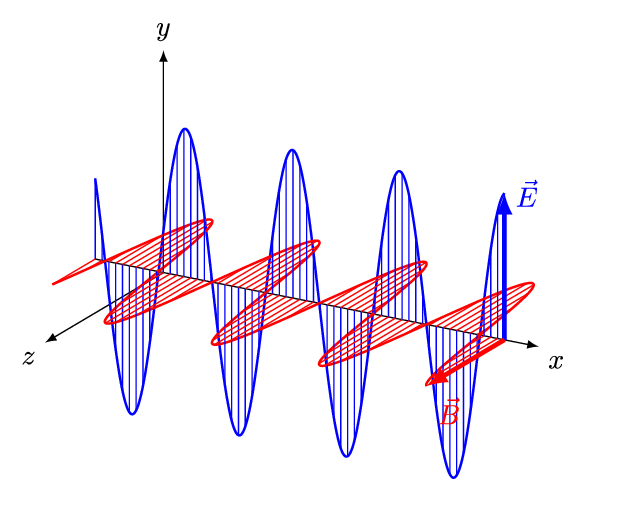
מקור: And1mu, CC BY-SA 4.0 https://creativecommons.org/licenses/by-sa/4.0, via Wikimedia Commons
אבל מניסיון אנו יודעים כי גל צריך להתקדם בתוך מֶדְיוּם, או תווך כלשהוא. למשל: גלי קול מתקדמים באוויר, במים, אפילו דרך קירות, אבל אין גלי קול בחלל הריק. גלי הקול שלכם הם למעשה התפשטות של תנודות בצפיפות האוויר (או כל תווך אחר שדרכו הקול מועבר). תצעקו על הירח חזק ככל שתרצו, אף אחד לא ישמע אתכם, כי בהיעדר אוויר בחלל ממילא אין שום דבר שאפשר לנדנד.
כנ"ל לגבי גלים בים: אלו תנודות של גובה פני המים, תנודות המתקדמות אל החוף במהירות מסוימת. הערה: שימו לב כי מה שמתקדם אל החוף זו רק ההפרעה בגובה פני המים; המים עצמם לא זזים לשום מקום, הם נעים אך ורק בכיוון מעלה-מטה.
המסקנה המתבקשת היא שאם האור הוא גל, אז הוא חייב לנוע בתוך מדיום או תווך מסוג כזה או אחר.
אוקיי, אז מה זה התווך הזה בדיוק? הסברה המקובלת באותה תקופה הייתה שהמדיום שבתוכו האור מתקדם נקרא: אֶתֶר, והוא ממלא כל המרחב שסביבנו. האֶתֶר ממלא לא רק את המרחב הריק בין הפלנטות, אלא את הכל: גם את המרחב שבין אטומים וגם את המרחב שבתוך האטומים. הכל כולל הכל; כל חלקיקי החומר ביקום, הם כמו דגים באוקיינוס עצום של אֶתֶר.
בדיוק בשלב זה נפל לפיזיקאים האסימון:
האֶתֶר עצמו יכול לשמש כמערכת יחוס אבסולוטית!
חשבו על כך: האתר ממלא את כל המרחב; כל מה שקיים, מונח או נע בתוך האתר. במילים אחרות: האתר הוא כמו לוח משבצות השחמט של היקום, וכל האובייקטים ביקום הם כמו כלי המשחק שמונחים ונעים על הלוח. רק מתבקש להגדיר כל תנועה ביקום ביחס לאתר!
פיזיקאים מאוד, מ-א-ו-ד אוהבים מצבים שכאלה: מודל פיזיקלי מוצלח (משוואות מקסוול) שממנו ניתן להסיק על קיומו של דבר מה חדש שלא נתגלה עד כה (אתר), לכן צריך לצאת "לשטח" ולנסות למצוא אותו! איזה כיף!
טובי הפיזיקאים מיד הפשילו שרוולים והחלו לתכנן ניסויים שיוכיחו כי אכן ניתן למדוד תנועה אבסולוטית ביחס לאתר.
הניסויים האלה (שעליהם ארחיב בפוסט הבא) דרשו מידה גבוהה מאוד של רגישות מדידה (רזולוציה), ואת מידת הרזולוציה הנדרשת אמנם אי אפשר היה להשיג באמצעות מעקב אחרי תנועה של גופים קשיחים, אבל כן ניתן היה להשיג באמצעות מדידה מדויקת של מהירות האור. במידה והניסוי יצליח – במידה וניתן יהיה למדוד תנועה אבסולוטית של האור ביחס לאתר – אז כנראה שהעיקרון של גלילאו תקף לחוקי המכניקה (לכל היותר), אך לא לחוקי האלקטרודינמיקה.
יעבוד? לא יעבוד?
אלא שלאיינשטיין הצעיר כבר התחילו ספקות לגבי מידת ההצלחה של הניסויים הנ"ל. מדוע?
בסוף המאה ה-19, בערך באותו זמן שבו טובי הפיזיקאים בעולם ניסו להשיג את הגביע הקדוש של מציאת האתר החמקמק ומדידה אבסולוטית של תנועה, איינשטיין היה תלמיד תיכון עם תשוקה רבה לפיזיקה.
באוטוביוגרפיה שלו, איינשטיין מספר על עצמו כיצד ערך ניסוי מחשבתי עוד כשהיה בתיכון בגיל 16 (איינשטיין מאוד אהב להסיק מסקנות מתוך ניסויי מחשבה שכאלה, והוא ערך ניסויים שכאלה גם בהמשך הקריירה שלו). בעיני רוחו, איינשטיין ניסה לדמיין כיצד תראה קרן אור לצופה הנע במקביל אליה במהירות הולכת וגדלה.
כאמור לעיל: קרן אור היא גל הנע במהירות האור. אם ניתן לקבוע את המהירות של אובייקטים באופן אבסולוטי ביחס לאתר, אז צופה הנע במקביל לקרן אור, ימדוד כיצד מהירות האור הולכת וקטנה ככל שהצופה מגביר את מהירותו.
זה בדיוק אותו דבר כמו אדם המנסה למדוד את המהירות של רכבת נוסעת, תוך כדי שהוא רודף אחריה: ככל שהאדם ירוץ יותר מהר, כך הרכבת תראה כנוסעת יותר ויותר לאט. באותו אופן, אם ננסה למדוד את מהירות האור תוך כדי שאנחנו "רודפים" אחריה, נגלה כי מהירות האור תלך ותקטן, כי גם לנו וגם לקרן האור יש מהירות אבסולוטית ביחס לאתר. בשורה התחתונה: מהירות האור תשתנה בהתאם למהירות הצופה.
איינשטיין לקח את הניסוי הנ"ל לקצה, והבין כי ברגע שבו הצופה "ישיג" את קרן האור – כלומר: גם הצופה ינוע במהירות האור – אז קרן האור תראה כאילו הפסיקה לנוע. במילים אחרות: הצופה יסתכל על גל "קפוא", גל שלא מתנדנד וגם לא מתקדם לשום מקום.
אבל איינשטיין כבר ידע שקיומו של גל אלקטרומגנטי "קפוא" סותר את משוואות מקסוול. במילים אחרות: גל "קפוא" אינו מהווה פתרון למשוואות מקסוול, ולא מקיים אותם. אולי גל שכזה מקיים חוקי פיזיקה אחרים, אבל לא את משוואות מקסוול.
איינשטיין לא היה מוכן לקבל את זה… כאמור לעיל, חוקי הפיזיקה צריכים להיות זהים ותקפים בכל מערכת ייחוס אינרציאלית. מבחינה היסטורית, היה זה גלילאו שהחיל את העיקרון הנ"ל על חוקי המכניקה בלבד (הוא עדיין לא הכיר את משוואות מקסוול), אבל איינשטיין חשב שיש להחיל את העיקרון של גלילאו גם על חוקי האלקטרודינמיקה.
זוהי למעשה האקסיומה הראשונה של תורת היחסות!!! תכלס, איינשטיין פשוט הכליל את העיקרון של גלילאו, וזו לא הכללה שבאותה תקופה היה מובן מאליו שמוצדק לעשות.
אם אתם רוצים להבין כמו שצריך את תורת היחסות של איינשטיין ואת הנושאים שאסביר בפוסטים הבאים, אז בראש ובראשונה תפנימו את זה: העקרון של גלילאו תקף לא רק לחוקי המכניקה של ניוטון, אלא גם לחוקי האלקטרודינמיקה של מקסוול.
לסיכום: למרות שטובי הפיזיקאים של אותה תקופה ניסו את כוחם במציאת האתר ומדידה מוצלחת של תנועה אבסולוטית, איינשטיין כבר החל לחשוד שהמשימה נידונה לכישלון: תנועה אחידה אבסולוטית אינה ניתנת לגילוי בשום דרך, כי כל חוקי הפיסיקה (מכניקה + אלקטרודינמיקה) זהים בכל מערכת אינרציאלית, וכל תופעה שנצפה בה תציית לאותם חוקים. אין מצב שנגלה תופעה מיוחדת שבאמצעותה נוכל להבדיל בין מערכת אינרציאלית אחת לאחרת.
זהו, עכשיו שאתם יודעים את האקסיומה הראשונה של תורת היחסות, עשיתם את הצעד הראשון בדרך להבנה של נושאים נוספים. בפוסט הבא אתמקד בניסיונות של הפיזיקאים לגלות את האתר, וכיצד תוצאות הניסוי הובילו את איינשטיין אל האקסיומה השנייה של תורת היחסות.
אל תלכו לשום מקום…
- במערכת אינרציאלית שכזו לא יפעלו כוחות מדומים שמתרחשים רק במערכת מואצת, לא-אינרציאלית [↩]



האם האקסיומה – פוסטולט – הראשונה של היחסות, נכונה?
האם לא נוכל לדעת את מהירותותינו יחסית לארץ לדוגמה, בקרון רכבת?
התשובה אני מאמין שלילית. נוכל למדוד את טמפרטורת קרינת הרקע, וזו יורדת באופן פרופורציוני למהירותינו יחסית למערכת המנוחה של קרינת הרקע. לכן אין בעיה לדעת מה מהירותינו יחסית לארץ.
כשהתאום מהפרדוקס נפגש עם אחיו הזקן, שניהם מסכימים על טמפרטורת קרינת הרקע ועל כן גם על גיל היקום. גם אם יש עשרה תאומים וכל אחד נע במהירות שונה, בזמן המפגש עם אחיהם הזקן כולם מסכימים על גיל היקום.
צ׳ט גיפיטי אומר שאם התאום המטייל נמצא במנוחה יחסית לקרינת הרקע אז במפגש הוא יהיה הזקן ואחיו שנשאר מאחור יהיה הצעיר.
ניתן להגיע למסקנה זו ישירות אם נעבור על מאמר היחסות המקורי של איינשטיין מ1905 ובפרק הראשון שעוסק בסינכרון שעונים מרוחקים, נחליף סינכרון באמצעות קרני אור כפי שמציע איינשטיין בסינכרון עיי מדידת הטמפרטורה או צפיפות פוטונים ליחידת נפח או כל שיטה אחרת שתכליתה לקבוע את גיל היקום, הזהה בכל נקודה ביקום.
נראה שאם מכשירינו מדוייקים מספיק, שעונינו יהיו מסונכרנים באותה המידה גם ללא הסינכרון באמצעות קרני אור שמהירותן זהה לכל מודד, שמהווה את הבסיס לתורת היחסות הפרטית.