מהו המטר? כיצד הוא הוגדר בעבר, וכיצד הוא מוגדר היום? התשובה לא ברורה מאליה, והניסיון להגדיר אותו במדויק לא היה פשוט בכלל. שני מתמטיקאים צרפתים כמעט שילמו על כך בחייהם תוך כדי הניסיון לעשות זאת. איך בדיוק? המשיכו לקרוא.
כולנו מכירים את סיפור המבול התנ"כי: בעקבות הדעיכה של האנושות לחיים של רשע ופשע, אלוהים התחרט על כל הפרויקט, והחליט לאתחל את המערכת מחדש; כל האנושות תושמד, חוץ מנח ומשפחתו. אלוהים פוקד על נח לבנות תיבה מעץ, ומציין במפורש את מידותיה:1
- אורך: 300 אמה.
- רוחב: 50 אמה.
- גובה: 30 אמה.
המקרא – למיטב ידיעתי – לא מגדיר במפורש מהי האַמָּה, אלא מניח שהקורא יודע במה מדובר. על פי ההגדרה המקובלת, האמה היא אורך היד, מהמרפק ועד קצה האצבע האמצעית.
יש לציין כי נח לא היה טרחן מספיק כדי לשאול את אלוהים באיזה יד בדיוק מדובר: של נח בעצמו, של אדם הראשון או שמא מדובר באורך ממוצע של יד אנושית. מכל מקום, דבר אחד אני יכול להבטיח לכם: אם אלוהים היה צריך להתעסק עם חברי האקדמיה הצרפתית למדעים של המאה ה-18, הוא היה מגלה שהחיים לא קלים כל כך. לכל הפחות הם היו מבקשים ממנו הגדרה מדויקת יותר, אך סביר להניח שהיו מסרבים להשתמש באמה באופן עקרוני, ובמקום זאת היו מציגים לאלוהים הצעה חלופית: המטר.
איך מֵטֶר נולד
זמן יחסית קצר לאחר המהפכה המדעית, התעורר הצורך לקבוע יחידות מידה קבועות ובלתי משתנות, כאלה המבוססות על תכונות יסודיות של הטבע. מכאן ברור מדוע האַמָּה אינה יכולה לשמש כיחידת אורך "טובה", מסיבות ברורות: השונות של האמה פשוט גדולה מדי, אין יד אנושית באורך אוניברסלי.
הניסיון הראשון להגדיר יחידת אורך אוניברסלית נעשה בסוף המאה ה-17, כמאה ועשרים שנה לפני הגדרת הקילוגרם, שעליו דיברנו בפוסט הקודם. הגדרת היחידה נעשתה בהתאם לפיזיקה של מטוטלת פשוטה, שהיא מערכת המורכבת מכדור קטן התלוי על חוט ומתנדנד מצד לצד, כך:

מקור: TheSonit, CC BY-SA 4.0 https://creativecommons.org/licenses/by-sa/4.0, via Wikimedia Commons
מטוטלת פשוטה היא מערכת שקל לנתח ולפתור באמצעות החוק השני של ניוטון. מפתרון המערכת, ניתן להסיק על תכונה יסודית של המטוטלת, והיא:
הזמן שלוקח למטוטלת להתנדנד מצד אחד לצד הנגדי, אינו תלוי במסה של הכדור שמחובר לחוט, אלא אך ורק באורך החוט ובעוצמת שדה הכבידה של כדור הארץ.
בגלל שעוצמת הכבידה היא תכונה אוניברסלית, אז אפשר להשתמש במטוטלת כדי להגדיר יחידת אורך! בהתאם לכך, האסטרונום הצרפתי ז'אן פִּיקַרְד (1620-1682), הציע את ההגדרה הבאה:
מטר אחד יוגדר בתור אורך החוט שעבורו לוקח למטוטלת בדיוק שניה אחת להתנדנד מצד אחד לצד שני.2
בשנים שלאחר מכן התברר כי הגדרה זו אינה טובה מספיק. הסיבה פשוטה: עוצמת הכבידה של כדור הארץ אינה קבועה, אלא משתנה ממקום למקום על פני כדור הארץ. כל עוד אין אפשרות למדוד ולהבחין בהבדלים אז אולי לאף אחד לא אכפת, אבל באותה תקופה יכולת המדידה הפכה למדוייקת מספיק. ז'אן רִישֶׁר (1630-1696), אסטרונום צרפתי נוסף, מדד הבדל של 0.3% בעוצמת הכבידה בין פריז לבין קָאיֶין (Cayenne), עיר הבירה של גינאה הצרפתית.
כמה מטרים מקו המשווה לקוטב הצפוני?
בעקבות כך, האקדמיה הצרפתית למדעים החליטה בסוף המאה ה-18 לעדכן את הגדרת המטר, באופן הבא:
מטר אחד יהיה שווה בדיוק ל- 1/10,000,000 של המרחק מהקוטב הצפוני אל קו המשווה, על גבי קו האורך שעובר דרך מצפה הכוכבים בפריז.3
כעת לא נותר אלא למדוד את המרחק מקו המשווה אל הקוטב הצפוני ולחלק ב- 10,000,000. איזה כיף.

מקור: US Government; adapted by User:Martinvl, Public domain, via Wikimedia Commons
טוב, די ברור שאי אפשר פשוט להתחיל מקו המשווה וללכת צפונה, לספור צעדים בדרך ולסיים בקוטב הצפוני. אבל למעשה, לא באמת צריך; בגלל שכדור הארץ עגול, מספיק למדוד רק חלק מהדרך, ולחשב את השאר. העיקרון יחסית פשוט: כל מה שצריך לדעת זה כמה מעלות צפונה מקו המשווה נמצאות נקודות ההתחלה והסיום של החלק הנמדד, כלומר: מהו קו הרוחב שלהן, נתון שאפשר לקבוע בשיטות אסטרונומיות. כפי שנראה מיד, ההפרש בין קווי הרוחב בתוספת המרחק המדוד בין נקודות ההתחלה והסיום, מאפשר לחשב את סך המרחק הכולל מקו המשווה לקוטב הצפוני.
המשימה הגדולה נפלה על שני מתמטיקאים בולטים מאותה תקופה: פְּייֶר מַאשֶן (1744-1804) וזָ'אן-בַפְּטיסְט דלַאַמְבֵּר (1749-1822). שני אלה היו צריכים למדוד במדויק את המרחק ממגדל הפעמון של כנסיית St-Eloi בעיר דנקרק בצרפת (קו רוחב 51.0356 צפון) ועד לטירת מוּנְז'וּאִיק בעיר ברצלונה בספרד (קו רוחב 41.363 צפון). כאמור לעיל, ההפרש בין קווי הרוחב הוא 10.75% מתוך 90 מעלות, שזה הפרש קווי הרוחב בין קו המשווה לקוטב הצפוני. לכן המרחק שימדדו דלאמבר ומאשן בין הכנסייה לטירה, הוא 10.75% מהמרחק הכולל מקו המשווה לקוטב הצפוני.4
גם במקרה זה, ברור כי מאשן ודאלמבר לא יכולים ללכת בקו ישר מדנקרק לברצלונה ולמשוך אחריהם חוט ארוך כדי למדוד את המרחק. הדרך רצופה בעצים, מבנים, תעלות ושלל אובייקטים שלא מאפשרים ללכת "דּוּךְ". אך למזלם, הם יכלו להתבסס על טריאנגולציה, שיטה למיפוי ומדידת תוואי קרקע שפותחה על ידי המתמטיקאי הגרמני וילברורד סְנֵל (1580-1626), ושימשה בהצלחה את ז'אן-דומיניק קסיני כדי למפות את כל צרפת בין השנים 1733 עד 1740; משימה שבעקבותיה פורסמה המפה המדויקת ביותר של צרפת עד אותה תקופה.
מכל מקום, המשימה של מאשן ודאלמבר ארכה כשש שנים (1792-1798), וכללה לא מעט קשיים: דאלמבר היה צריך להתמודד עם כפריים שחשבו כי הוא מכשף, ומכשירי המדידה שלו נועדו להטיל עליהם קללה; זה לא צחוק, דברים כאלה יכולים לתקוע את כל העסק. בנוסף, צרפת הכריזה מלחמה על ספרד ב-1793, ושכחה לעדכן את מאשן. המסכן מצא את עצמו בכלא הספרדי לתקופה מסויימת, אחרי שנחשד בריגול לטובת צרפת.
למרות הכל, בסוף הם הצליחו, ועל פי תוצאת החישובים התקבל כי המרחק מקו המשווה אל הקוטב הצפוני הוא בדיוק 10,261,480 מטרים "ישנים" (כלומר, מטר של מטוטלת). כאמור לעיל, המטר החדש הוא 1/10,000,000 מהמספר הנ"ל, ולכן:
\(\displaystyle {\frac{{10,261,480}}{{10,000,000}}=1.026148}\)
במילים פשוטות: המטר החדש ארוך פי 1.026148 מהמטר הישן.
היישום הממשי לא איחר לבוא, ובשנת 1799 נוצר האבטיפוס הראשון של המטר: מוט פלטינה באורך מטר אחד בדיוק, על פי ההגדרה העדכנית. המוט הנ"ל הפך להיות המטר, בה"א הידיעה, ונשמר בארכיון הלאומי ביחד עם גליל הפלטינה שמגדיר את הקילוגרם, שנוצר אף הוא באותה שנה, כפי שתיארנו בפוסט הקודם. גם המטר – בדומה לקילוגרם – עבר שדרוג מסוים בשנת 1876 עם הקמת הלשכה הבינלאומית למידות ומשקלות. נוצר מוט חדש – זהה עד כמה שאפשר למקור – מתערובת של פלטינה ואירידיום, ושלושים העתקים שלו פוזרו ברחבי העולם למדינות שונות.
המון המון אורכי-גל
הגדרת המטר נשארה ללא שינוי עד שנת 1960, אז המטר הוגדר מחדש בעקבות פריצות דרך משמעותיות שנעשו בתחילת המאה העשרים. ההגדרה החדשה משתמשת בתכונה יסודית של האור, תכונה הנקראת: אורך-גל. במה מדובר?
אם תדמיינו גל במים ותנסו לתאר אותו, תוכלו בקלות לראות כי הגל הוא למעשה הפרעה של גובה פני המים, הפרעה המתקדמת אל החוף. קרן אור מתנהגת באופן דומה למדי: גם קרן אור היא התקדמות של הפרעה אך לא במים, אלא בשדה החשמלי-מגנטי. אורך-גל זה פשוט המרחק בין פסגה אחת של הגל, אל זו שלאחריה, כפי שניתן לראות באנימציה הבאה:
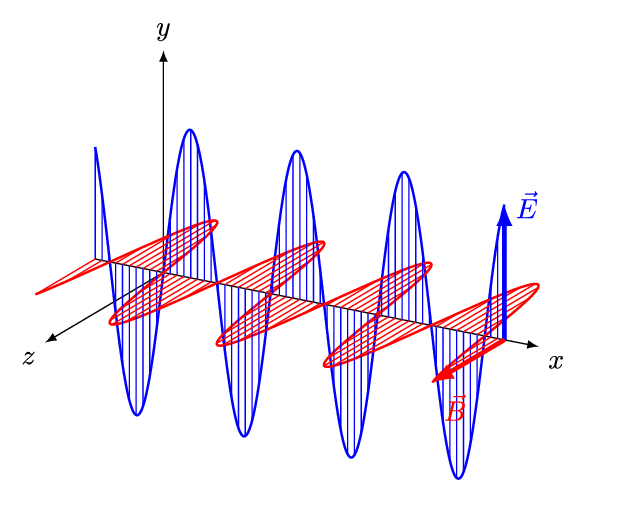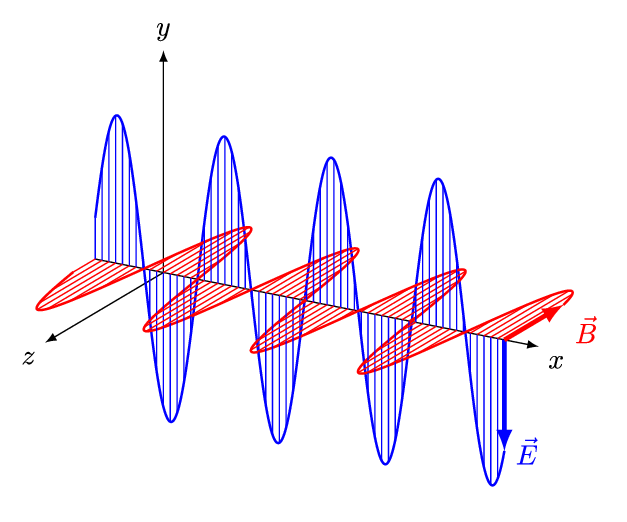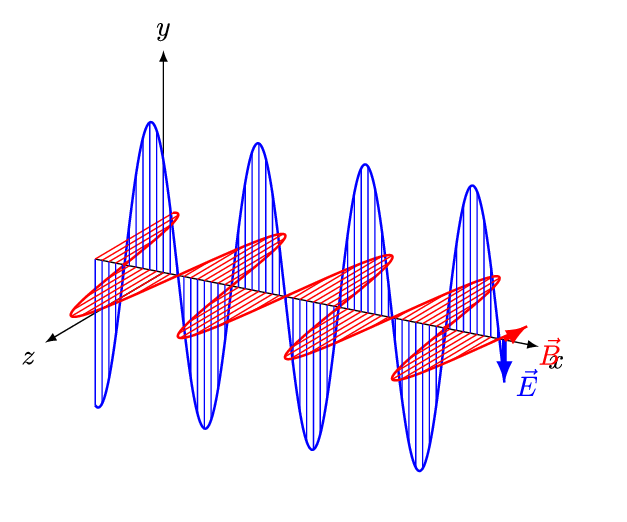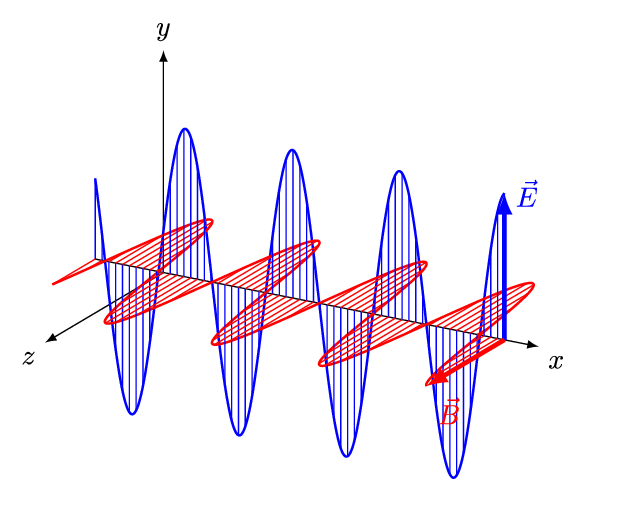
מקור: And1mu, CC BY-SA 4.0 https://creativecommons.org/licenses/by-sa/4.0, via Wikimedia Commons
רק לשם המחשה מהו סדר הגודל של האורכים שעליהם אני מדבר: אורך-גל של אור בתחום הנראה גדול בערך פי 2000 מגודלה של מולקולת מים בודדת.
איך כל זה קשור להגדרת המטר? מסתבר כי בעזרת שיטת מדידה הנקראת אינטרפרומטריה, יכולת הדיוק שלנו במדידת מרחקים השתפרה פלאים; השיטה הזו מאפשרת לנו לספור אורכי-גל, פשוטו כמשמעו. אנסה לתמצת את השיטה במילים פשוטות, כדי שתבינו במה מדובר:
- ניתן לקחת קרן אור ממקור אחד, ולפצל אותה לשתי קרניים באמצעות מראה מיוחדת.
- כל אחת מהקרניים ממשיכה להתקדם במרחב לאורך מרחק שונה, עד לנקודה שבה הקרניים מאוחדות שוב על גבי מסך.
- בגלל האופי הגלי של האור, מתקבל מצב בו הפרש הדרכים יכול לגרום לשתי קרני האור לבטל אחת את השניה (כך שמתקבל על המסך חושך מוחלט) או להעצים אחת את השניה (כך שמתקבל על המסך אור בוהק).
- כעת ניתן לשנות באופן רציף את הפרש הדרכים היחסי בין שתי הקרניים, כך שעל המסך מתקבלים כתמי אור וחושך לסירוגין.
- באמצעות מעקב קפדני על מספר הפעמים שבהם אור התחלף לחושך ולהיפך, ניתן לעקוב – ממש לספור – כמה אורכי-גל צברנו בזמן השינוי הרציף של הפרש הדרכים!5
באנימציה הבאה תוכלו לראות איך נראים על המסך כתמי האור\חושך המתחלפים תוך כדי שינוי הפרש הדרכים בין שתי הקרניים:

מקור: Skilbride21, CC BY-SA 4.0 https://creativecommons.org/licenses/by-sa/4.0, via Wikimedia Commons
לצורך הגדרה זו, נבחר היסוד קריפטון.6 יסוד זה פולט – תחת תנאים מסוימים – אור בגָּוֶן מאוד ספציפי של כתום, וכל שנשאר לעשות זה להגדיר כמה אורכי-גל נמצאים במטר בודד. את אורכי-הגל נוכל לספור – אחד אחד – בעזרת השיטה האינטרפרומטרית שתיארנו לעיל. בשורה התחתונה, זו הגדרת המטר כפי שנבחרה ב-1960:
מטר בודד שווה ל- 1,650,763.73 אורכי-גל של אור כתום הנפלט מהיסוד קריפטון בטמפרטורה של 64 מעלות קלווין.
מעניין לשים לב לדמיון בין השיטה הזו לבין השיטה שבה ספרנו אטומי פחמן כדי להגדיר את הקילוגרם בפוסט הקודם; אורכי-גל של אור הם כמו "אטומים" של אורך שבאמצעותם ניתן להגדיר את המטר!
מה, גם זה לא טוב?
פיזיקאים כידוע הם טיפוסים הפכפכים מטבעם, לכן אין זה מפתיע שלקח להם בדיוק 23 שנים להתחרט, ושוב פעם לשנות את ההגדרה של המטר. גם הפעם, נעשה שימוש בתכונה יסודית של האור, אך במקרה הזה לא באורך-גל, אלא במהירות האור. כאן העסק הופך להיות טיפה מבלבל.
מהירות האור בוואקום – למיטב ידיעתנו – היא תכונה קבועה, ובלתי משתנה של הטבע. בהתאם לזאת, הפיזיקאים טוענים את הטענה הבאה:
אם אנו יודעים כי מהירות האור בוואקום היא 299,792,458 מטרים לשנייה, אז נוכל להגדיר את המטר בתור המרחק שעובר אור בוואקום במשך 1/299,792,458 של שנייה.
במילים פשוטות: קחו שניה אחת, וחלקו אותה ל- 299,792,458 חלקים שווים. המרחק שעובר האור במשך חלק אחד – זה המטר!
אוקיי, מיד ברור כי הגדרת המטר לא תושלם עד שלא נגדיר גם מהי שניה אחת. בפוסט הבא נעסוק בהגדרה המדויקת של שניה, אבל זה ענין טכני ואפשר לשים אותו לרגע בצד, לא כאן הבעיה.
אז מה לא בסדר? ובכן, במבט ראשון, משהו בהגדרת המטר שתיארנו לעיל נראה עקום לגמרי. זה נשמע כמו טיעון מעגלי: פיזיקאים מודדים את מהירות האור במטרים לשניה, ואז משתמשים במהירות האור להגדיר חזרה את המטר??? הזוי משהו, לא?
אלא שהכל כשר למהדרין ואין לכם מה לדאוג. מדוע? הפיזיקאים נוקטים כאן בגישה של "הפוך-על-הפוך". במילים פשוטות: האור ביחידת זמן אחת (לא משנה איזה) מתקדם במרחב מרחק נתון (לא משנה באיזה יחידות). אנו למעשה מגדירים את המטר (וגם את השנייה) באופן כזה שיכריח את מהירות האור להיות 299,792,458 מטרים לשנייה! בשיטה זו אנו קובעים מראש את ערכה של מהירות האור, והיא אינה יכולה לקבל שום ערך אחר! ערכה תמיד יהיה 299,792,458 מטרים לשניה, כי המטר והשניה מוגדרים בדיוק באופן הדרוש לכך. הבנתם?
סיכום
אז מה היה לנו עד עכשיו?
בפוסט הקודם הגדרנו את הקילוגרם, אך ראינו כי ההגדרה שלו דורשת הגדרה מדויקת של המטר והשניה גם יחד.
בפוסט הנוכחי הגדרנו את המטר, אך גילינו כי המטר עצמו דורש הגדרה מדויקת של השניה.
אז כמה זמן בדיוק אורכת שניה אחת? על השאלה הזו אענה בפוסט הבא.
- בראשית, ו:טו [↩]
- השניה כבר הייתה מוגדרת באותה תקופה כ- 1/3600 של שעה, והשעה כ- 1/24 של היממה. בנוסף, השם המקורי של יחידת האורך שהציע פיקרד לא היה מטר אלא toise. אני לא מכיר לזה תרגום בעברית, ונראה לי שמבטאים את זה כך: twaz (טוואז). הטוואז במקור הוגדר כשווה לפעמיים אורך החוט של המטוטלת, כך שלמעשה טוואז אחד שווה לשני מטרים, אך פרט זה אינו חשוב במיוחד, כי היחס בין הטוואז למטר מוגדר היטב. כמו כן, יש לזכור כי בהתאם להגדרה זו המטר נקבע על ידי ניסוי, לא על ידי חישוב. למה הכוונה? מסתבר כי מבחינה מתמטית, אורך החוט של מטוטלת שחצי זמן המחזור שלה הוא שניה אחת, שווה לעוצמת הכבידה g=9.8 חלקי פאי בריבוע. מסתבר כי היחס הזה שווה ל-0.993, כלומר יחס מאוד קרוב ל-1, אך לא בדיוק. הסיבה לכך היא כי הערך g=9.8 מובע ביחידות של מטר לשניה בריבוע, ולכן הערך של g כבר מתבסס על ההגדרה המודרנית של המטר, לא על הגדרת המטוטלת, לכן מטר אחד על פי הגדרת המטוטלת קצר מעט מהמטר המודרני. [↩]
- קו זה נקרא: המרידיאן של פריז. [↩]
- זה כמובן חישוב פשטני המתבסס על ההנחה שכדור הארץ עגול לחלוטין. זו הנחה שגויה, ולמעשה כדור הארץ הוא בצורה של אליפסואיד, בדומה לכדור שפחוס מעט בקטבים. מסיבה זו החישוב הופך להיות מורכב יותר מבחינה מתמטית, אך אפשרי בהחלט. [↩]
- במקרה של אינטרפרומטר בקונפיגורצית מייקלסון, ניתן להראות כי כל פעם שאור התחלף לחושך ולהיפך, הפרש הדרכים גדל ברבע אורך-גל. בניסוח מדויק יותר: הפרש הדרכים שווה לחצי אורך-גל כפול הפרש הפאזה בין הקרניים לחלק לשני פאי. [↩]
- מדובר על האיזוטופ קריפטון-86. [↩]


