מי היה יוֹהָנְס קֶפּלֶר? מהם שלושת החוקים שניסח ואיך הם שינו את ההבנה שלנו על מערכת השמש? ומה הקשר בין הוותק של מנחה באקדמיה להצלחה של הסטודנטים שלו? כל התשובות, בפוסט לפניכם.
כשהתחלתי את לימודי הדוקטורט, אפשר לומר כי במובן מסוים היה לי יותר מזל משכל. הסיבה לכך פשוטה: המנחה שלי בדיוק החל את שנתו הראשונה באוניברסיטה כחוקר. איך זה קשור, אתם שואלים?
ובכן, למי שלא יודע, מנחה צעיר פשוט לא יכול לתת לסטודנטים שלו להיכשל, כך שזכיתי לכל התמיכה וההדרכה שאפשר לקבל. באופן כללי ניתן לומר, כי הצלחת הסטודנטים היא גם הצלחת המנחה. אמירה זו נכונה גם למנחים ותיקים כמובן, אך למנחים צעירים היא נכונה כפליים, פשוט כי מנחה צעיר עדיין לא קיבל את הקביעות הנכספת באוניברסיטה… זאת בניגוד למנחים וותיקים, שלא חוששים לזרוק את הסטודנטים שלהם למים העמוקים בלי מצופים.
מכל מקום, המזל האקדמי שלי לא היה מנת חלקו של יוֹהָנְס קֶפּלֶר (1571-1630), המתמטיקאי הגרמני שעליו – ועל שלושת החוקים שלו – נלמד במאמר הנוכחי. כפי שתראו להלן, די ברור כי לקפלר היה יותר שכל מאשר מזל; בעזרת הכישרון האינטלקטואלי שלו, קפלר הצליח לדלג מעל המשוכות האקדמיות, ולקדם במידה משמעותית את ההבנה שלנו על מערכת השמש.
מעשה במַנְחֶה ותיק וסטודנט צעיר
מגיל צעיר קפלר הראה כישרון למתמטיקה, ובגיל 22 החל לעבוד כמורה למתמטיקה ואסטרונומיה בבית ספר פרוטסטנטי בעיר גראץ שבאוסטריה. לרוע המזל, תהפוכות פוליטיות ודתיות של אותה תקופה לא אפשרו לקפלר להישאר, והוא נאלץ לעזוב. להפתעתו, קפלר שמע על משרה בפראג כעוזר מחקר של האסטרונום הדני טִיכּוֹ בְּרָאהֵה (1546-1601), והוא קפץ על ההזדמנות.
באותה תקופה, טיכו נחשב לאסטרונום המוכשר ביותר באירופה. במילים אחרות: טיכו היה פשוט מקצוען מהשורה הראשונה, ולא היו לו מתחרים בכל מה שקשור לאיכות התצפיות ודיוק המדידות. לטיכו היה את ציוד המדידה המתקדם ביותר, וטיכו עצמו תכנן ובנה חלק גדול מהמכשור בו השתמש.
פה מתחיל החלק המעניין: טיכו הקפיד שלא לחשוף את קפלר להיקף המלא של התצפיות והמדידות שביצע. מדוע? באותה תקופה, לטיכו היה מודל פרטי משלו למערכת השמש, מעין גרסה היברידית בין המודל הגֵּאוֹצְטֵרִי של קלאודיוס תַּלְמַי והמודל ההֶלְיוֹצֶנְטְרִי של קופרניקוס, וטיכו עבד קשה מאוד כדי להתאים את התצפיות שביצע אל המודל שלו.1 יש אומרים כי טיכו קלט די מהר עד כמה קפלר מוכשר, ולכן פחד כי אם קפלר יקבל גישה מלאה לנתונים, אז בסופו של דבר קפלר יצליח איפה שטיכו נכשל, ויאפיל עליו בהישגיו. עקב כך, טיכו שמר את הקלפים קרוב לחזה, וחשף את קפלר רק לנתונים שאסף על המסלול של מאדים – מסלול שהיה קשה במיוחד להתאים למודל של טיכו – בתקווה שקפלר ישבור את הראש ויתקדם לאט, אם בכלל.
כפי שתראו להלן, צחוק הגורל הוא שטיכו – בלי לשים לב – חשף בפני קפלר דווקא את הקלפים שעזרו לקפלר לנסח את שלושת החוקים המפורסמים שלו, להבין טוב יותר את מבנה מערכת השמש, ולמוטט סופית את המודל של טיכו עצמו!
אז מהם שלושת החוקים של קפלר? אסביר אותם להלן אחד לאחד, כך שלא ישאר לכם ספק במה מדובר.
החוק הראשון
בראש ובראשונה, קפלר הבין כי קופרניקוס אמנם צדק כשטען כי כוכבי הלכת מקיפים את השמש, אך הוא טעה בכך שחשב כי מדובר במסלול מעגלי. על פי קפלר, המסלול אינו מעגלי, והבנה זו היא החוק הראשון של קפלר:
כוכבי הלכת מקיפים את השמש במסלול אליפטי כאשר השמש נמצאת באחד ממוקדי האליפסה.
כדי לא להשאיר את העסק מעורפל, אזכיר בקצרה את ההבדל בין מעגל לאליפסה:
על גבי מעגל, המרחק של כל נקודה מהמרכז הוא קבוע. אך בניגוד למעגל, לאליפסה יש שני "מרכזים", או: מוקדים. לכן על גבי אליפסה, מה שקבוע הוא המרחק הכולל של כל נקודה משני המוקדים יחד.
לפי ההגדרה לעיל, אפשר בקלות לצייר אליפסה באמצעות עפרון, שני נעצים, ולולאת חוט; האנימציה הבאה ממחישה זאת היטב:

מקור: مازیار کیوان, CC BY-SA 4.0 https://creativecommons.org/licenses/by-sa/4.0, via Wikimedia Commons
כאמור לעיל, אף על פי שכוכבי הלכת כולם נעים במסלול אליפטי, עדיין מדובר באליפסות שונות, חלקן פחוסות יותר וחלקן פחות.2 לדוגמה:
- המסלול של נוגה הוא כמעט מעגלי, וקשה מאוד להבחין שמדובר בכלל באליפסה.
- המסלול של כוכב חמה פחוס במידה ניכרת, ונראה ממש כמו ביצה.
- לכוכבי שביט יש מסלולים מאוד פחוסים, ונראים כמו גומייה שתפסו אותה בשני קצותיה ומתחו אותה חזק.
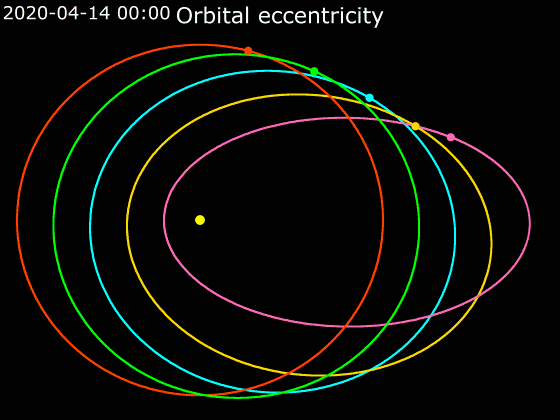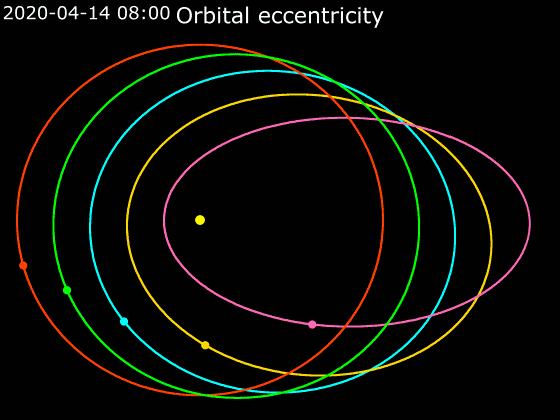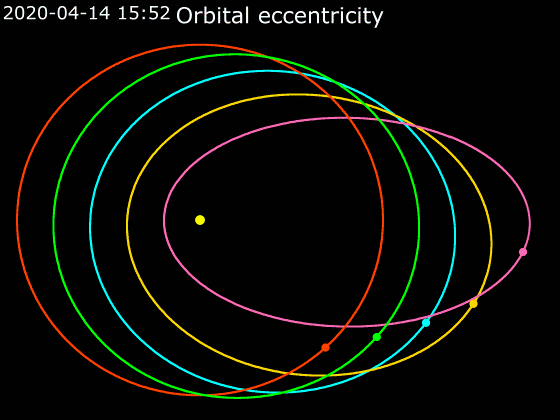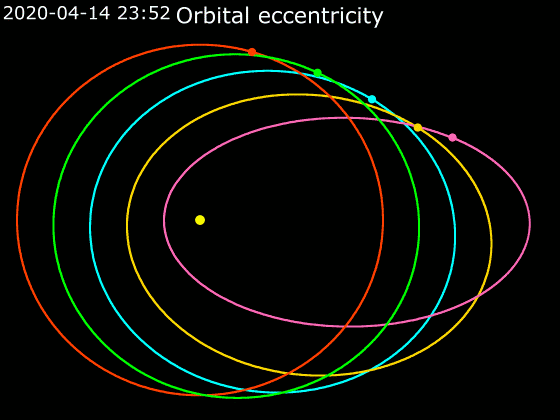
מקור: Phoenix7777, CC BY-SA 4.0 https://creativecommons.org/licenses/by-sa/4.0, via Wikimedia Commons
מסתבר כי לטיכו לא היו תצפיות נרחבות על כוכב חמה, אך על מאדים היה לטיכו שפע של מידע, והמסלול של מאדים הוא האליפטי ביותר אחרי כוכב חמה. כל המודלים הקדומים של מערכת השמש – כולל של טיכו עצמו – הניחו מראש כי כל המסלולים של כוכבי הלכת חייבים להיות מעגליים, וזו אחת הסיבות מדוע טיכו התקשה להתאים את התצפיות למודל שלו. אלא שטיכו הגיש לקפלר על מגש של כסף את המסלול האליפטי ביותר שהיה לו…
החוק השני
אילו המסלול של כוכב לכת סביב השמש היה מעגלי באופן מושלם, אז הוא היה נע סביב השמש במהירות קבועה, וגם המרחק שלו מהשמש היה קבוע. אך על פי החוק הראשון של קפלר, המסלול אינו מעגלי אלא אליפטי, ולכן גם המרחק של כוכב הלכת מהשמש וגם המהירות שלו משתנים לאורך המסלול. במילים פשוטות: קרוב לשמש המהירות גדולה, ורחוק מהשמש המהירות קטנה. עובדה זו הביאה את קפלר לנסח את החוק השני שלו:
הקו שמחבר את כוכב הלכת עם השמש מכסה שטחים שווים במרווחי זמן שווים.
אוקיי, כדי שתבינו מה המשמעות של החוק השני, הכנתי לכם תמונה בה תוכלו לראות את מסלול כדור הארץ סביב השמש במבט "מלמעלה", ואת מיקום כדור הארץ בתחילת כל חודש, מינואר ועד יולי.3 ניתן לראות כי בדרך זו חילקנו את האליפסה לגזרות, כמו מגש פיצה המחולק למשולשים.
ופה הפאנץ'-ליין:
אמנם במבט ראשון זה לא נראה כך, אך קפלר הבין כי לכל גזרה יש בדיוק את אותו השטח!

זכרו כי במסלול אליפטי, כדור הארץ נע מהר כשהוא קרוב לשמש (במהלך חודש ינואר) ולאט כשהוא רחוק ממנה (במהלך חודש יוני). אם נסתכל על הדרך שכדור הארץ עובר על האליפסה עצמה, נקבל כי כדור הארץ עובר דרך ארוכה יותר לאורך חודש ינואר, וקצרה יותר לאורך חודש יוני. אך אם נסתכל על שטח הגזרה שנוצר במהלך התנועה החודשית, נקבל כי שטח הגזרה זהה בכל חודש וחודש.4
חשוב להבין כי החלוקה לחודשים היא שרירותית לגמרי. במילים פשוטות: לא חייבים לחלק את האליפסה ל-12 גזרות, כמספר חודשי השנה, אפשר לחלק את האליפסה לכמה גזרות שרק תרצו; כל עוד החלוקה מתבצעת במרווחי זמן שווים, תמיד נקבל כי לכל גזרה יש בדיוק את אותו שטח.
החוק השלישי
אמנם טיכו לא חשף בפני קפלר את מלוא הנתונים שאסף, אך טיכו מת במפתיע שנה אחת לאחר שקפלר החל לעבוד אצלו, כך שלבסוף קפלר קיבל גישה מלאה למידע. בזמן שקפלר חקר את המסלולים של שאר כוכבי הלכת, הוא שם לב לקשר מעניין בין זמן ההקפה של כוכב לכת למבנה הגאומטרי של המסלול האליפטי שלו. הבנה זו הביאה את קפלר לנסח את החוק השלישי:
לכל כוכבי הלכת, קיים יחס זהה בין ריבוע זמן המחזור לחזקה השלישית של המרחק הממוצע מהשמש.
אז מה זה אומר בדיוק? כדי להבין את החוק השלישי של קפלר, יש להגדיר במפורש שני מושגים:
- זמן המחזור: הזמן הכולל שלוקח לכוכב לכת לבצע הקפה אחת סביב השמש. לדוגמה: כדור הארץ משלים הקפה אחת ב-365 ימים. מאדים עושה זאת ב-687 ימים, וכן הלאה. נסמן את זמן ההקפה באות \(T\).
- המרחק הממוצע מהשמש: הערך הממוצע בין המרחק הקצר ביותר והארוך ביותר של כוכב לכת מהשמש. לדוגמה: כדור הארץ נמצא הכי קרוב לשמש בתחילת ינואר, והכי רחוק ממנה בתחילת יולי. הממוצע של שני המרחקים הללו – הקצר והארוך – הוא 150 מיליון ק"מ, וזה המרחק הממוצע של כדור הארץ מהשמש. למאדים יש מרחק ממוצע של 228 מיליון ק"מ וכן הלאה. נסמן את המרחק הממוצע באות \(a\).5
קפלר גילה כי היחס בין החזקה השלישית של המרחק הממוצע, \({a^3}\), לבין ריבוע זמן המחזור, \({T^2}\), הוא מספר קבוע ומשותף לכל כוכבי הלכת. הדרך הטובה ביותר לראות זאת היא להסתכל על המספרים עצמם, ובטבלה להלן סיכמתי מספר דוגמאות. לכל כוכב לכת בטבלה, ניתן לראות את זמן ההקפה \(T\) (בימים), את המרחק הממוצע \(a\) (במיליוני ק"מ), ואת היחס: \(\frac{{{a^3}}}{{{T^2}}}\) :
| כוכב לכת | זמן הקפה T (ימים) | מרחק ממוצע a (מיליוני ק"מ) | יחס a3/T2 |
| נוגה | 224.701 | 108.208 | 25.0939 |
| כדור הארץ | 365.256 | 149.598 | 25.0947 |
| צדק | 4,332.59 | 778.479 | 25.1331 |
| אורנוס | 30,688.5 | 2870.972 | 25.1267 |
שימו לב כי היחס שמתקבל בעמודה השמאלית אינו זהה לחלוטין לכל כוכבי הלכת בטבלה. יש לכך סיבה טובה, אך כדי לא להעמיס על הפוסט, הרחבתי על כך בקישור נפרד כאן, לכל מי שרוצה להתעמק בנושא. מכל מקום, היחס הנ"ל נשמר לכל כוכבי הלכת, כולל כוכבי לכת ננסיים כגון: צֵרֶס (Ceres) שנמצא בין מאדים לצדק, ואֵרִיס (Eris), כוכב ננסי עם מסלול מאוד אליפטי שנמצא רחוק מאוד מהשמש, אחרי פלוטו.
כשקפלר שם לב לתכונה הזו, הוא התרשם עמוקות. היחסים והפרופורציות החבויים בתנועתם של גופים במערכת השמש נתפסו במחשבתו של קפלר בתור "מוזיקה שמיימית", כביכול הקוסמוס מנגן ומסלוליהם של כוכבי הלכת הם המיתרים שלו.
סיכום
עבודתו ומסקנותיו של יוהנס קפלר קידמו את ההבנה שלנו על מערכת השמש בצורה בלתי רגילה. מבחינת המדע, חוקי קפלר נחשבים ל- "קפיצה הגדולה" שבאה אחרי ההבנה של קופרניקוס שהשמש נמצאת במרכז המערכת ולא כדור הארץ. כמאה שנים לאחר מכן, אייזק ניוטון פרסם את חוקי התנועה המפורסמים שלו, ובעזרתם הצליח לשחזר מתמטית את החוקים של קפלר, שנקבעו מלכתחילה באופן אמפירי בלבד.
- המודל של טיכו מיקם את כדור הארץ במרכז, כך שהשמש והירח מקיפים את כדור הארץ (בדומה למודל של תלמי), אך שאר כוכבי הלכת מקיפים את השמש (בדומה למודל של קופרניקוס). [↩]
- עד כמה האליפסה פחוסה או "עגולה", ניתן לדעת על פי הערך של מקדם האקסצנטריות הנע בין 0 ל-1. [↩]
- ליתר דיוק, כדור הארץ נמצא הכי קרוב לשמש בתחילת ינואר, ב-3 או ב-4 לינואר, אך ניתן להתעלם מכך כרגע. לצורך הפשטות, נניח כי המרחק הקצר ביותר לשמש מתקבל בדיוק ב-1 לינואר [↩]
- יש לשים לב כי לפי הלוח הגריגוריאני משך הזמן של כל חודש אינו זהה. יש חודשים עם 30 ימים, 31 ימים או 28. אך כל זה לא קריטי להבנת החוק השני של קפלר. לצורך הענין, אפשר להניח כי משך כל חודש הוא 30.436875 ימים, שזה האורך הממוצע של כל חודש. [↩]
- המרחק הממוצע a שווה – על פי הגדרה – למחצית הציר הראשי של האליפסה. הציר הראשי הוא אורך הקו העובר בין שני המוקדים, ומחבר בין שני הקצוות המרוחקים ביותר של האליפסה. במילים אחרות: הציר הראשי הוא למעשה "הקוטר" הארוך של האליפסה. מכאן נובע כי הציר הראשי הוא הסכום של המרחק הקצר ביותר והארוך ביותר מהמוקד. לכן מחצית הציר הראשי הוא הערך הממוצע בין המרחק הקצר ביותר והארוך ביותר. יש דרכים נוספות לחשב את המרחק הממוצע, והרחבתי על כך בקישור כאן, אך החוק השלישי של קפלר מתייחס למחצית הציר הראשי של האליפסה. [↩]



שאלה: אם השמש נמצאת במוקד אחד של האליפסה, מי/מה נמצא במוקד השני?
כלום, למיטב ידיעתי, ואם היה משהו היינו רואים אותו חולף על פני השמש בתחילת יולי, מתי שכדור הארץ הכי רחוק מהשמש. בנוסף, המיקום של המוקד השני אינו זהה לכל כוכבי הלכת. לכל כוכב לכת יש מוקד שני במיקום שונה.
שכוייח 🙂