נסו לחפש טיסה ישירה בין ספרד לניו-זילנד. לא תמצאו, כי אין; המרחק פשוט גדול מדי. תצטרכו לעצור בדרך לפחות פעם אחת – בסן פרנסיסקו למשל – וגם אז המסע כולו יהיה ארוך ומתיש, יותר מ-26 שעות במצטבר של זמן טיסה. אבל יש דרך להגיע מספרד לניו-זילנד הרבה יותר מהר. איך בדיוק? כל התשובות, בפוסט לפניכם.
התובנה כי הארץ אינה שטוחה אלא כדורית, התקבלה בקרב המלומדים עוד בתקופת יוון העתיקה. לדוגמה: האסכולה הפיתגוראית, העלתה לטובת הרעיון נימוקים מתמטיים באופיים, בעוד אריסטו כבר ביסס את הרעיון על סמך תצפיות ממשיות.1 אף על פי כן, מלומדי העת העתיקה עדיין נאלצו להתמודד עם השאלה כיצד בדיוק הם פני הדברים בצד השני של כדור הארץ. בראש ובראשונה, האם בכלל ניתן להניח על קיומם של בני אדם באותם אזורים מרוחקים.
בני אדם אלו – שאולי קיימים או לא בצד השני של כדור הארץ – נקראו בשם "אנטיפודים", שם שמקורו בשפה היוונית: אנטי פירושו: כנגד, ופודוס פירושו: רגליים. במילים אחרות: אלו בני אדם שנמצאים כנגד הרגליים שלנו, כלומר מהצד השני של כדור הארץ.
במאות השנים לאחר מכן, בתקופת ימי הביניים, המלומדים הנוצרים אימצו – על פי רוב – את ההבנה שהארץ אכן כדורית, אך הם לא ממש אהבו את הרעיון כי ישנם בני אדם בצד השני של כדור הארץ. הסיבה לכך פשוטה: אם אכן קיימים בני אדם שכאלה, נראה כי בלתי אפשרי להגיע אליהם. ראשית מפני שחציית האוקיינוס נראתה כבלתי אפשרית באותה תקופה. שנית, האמונה הרווחת הייתה כי החום בקו המשווה הוא בלתי נסבל, וממילא אי אפשר לחצות אותו לצד השני. מכל מקום, קיומם של בני אדם אנטיפודים יוצר בעיה חמורה: הלא בשורתו של ישו אמורה להגיע לכל בני האדם ולגאול אותם, כולל אלו שאולי קיימים בצד השני. אם לא ניתן להגיע אליהם, אז מסכנים אלה לא יוכלו להיגאל לעולם! בהתאם לכך, האפיפיור זכריה (679-752) אכן הכריז במאה השמינית כי אמונה ברעיונות כאלה היא בגדר כפירה.
מה זאת אומרת איפה? מול הרגליים שלך!
מכל מקום, המונח אנטיפודים הושאל כדי לתאר את אותם בני אדם שאולי קיימים ואולי לא, אך משמעותו העיקרית של המונח היא גיאומטרית:
על פני השטח של כדור, שתי נקודות נקראות אנטיפודיות אם הקו הישר המחבר ביניהן, עובר דרך מרכז הכדור.
במילים פשוטות: אם תמתחו קו ישר מהרגליים שלכם דרך מרכז כדור הארץ, אז בנקודה שבה הקו יצא מהצד השני של כדור הארץ, נקודה זו היא הנקודה האנטיפודית שלכם.
לפי הגדרה זו, מהי הנקודה האנטיפודית של מדינת ישראל? ובכן, אם תתחילו לחפור בקרקע של ישראל עמוק יותר ויותר לכיוון מרכז כדור הארץ, בסוף אכן תצאו מהצד השני, אך תמצאו את עצמכם בלב האוקיינוס השקט. ברור מאליו כי תופעה זו אינה יוצאת דופן: אין הרבה מקומות יבשתיים בעולם שגם הנקודה האנטיפודית שלהם נמצאת ביבשה. הסיבה לכך ברורה: כ-70% מפני כדור הארץ מכוסים במים, לכן רוב הסיכויים שאם תתחילו לחפור בקרקע, אז בצד השני תמצאו את עצמכם בלב ים.
כדי לראות את כל שטחי היבשה שיש להם נקודה אנטיפודית שגם היא נקודה יבשתית, נצטרך להסתכל על מפת העולם כאשר היבשות מוצגות על המפה פעמיים: פעם אחת בצורתן הרגילה, ופעם נוספת כפי שהן מוטלות על הצד השני של כדור הארץ. אם מעולם לא ראיתם מפה שכזו, שווה להקדיש לה דקה של התבוננות. כדי שתפיקו את המירב מהמפה המוזרה הזו, שימו לב לדברים הבאים:
- צבע אדום: אלו היבשות בצורתן הרגילה, כפי שהן מופיעות במפה העולמית הסטנדרטית שכולכם מכירים.
- צבע צהוב: אלו היבשות כפי שהיו מופיעות אם היינו מטילים אותם על הצד השני של כדור הארץ. קחו לדוגמה את יבשת אוסטרליה: היבשת עצמה נמצאת בצד ימין של התמונה בצבע אדום, אך אוסטרליה האנטיפודית מופיעה בצבע צהוב באמצע האוקיינוס האטלנטי, בין אפריקה למרכז אמריקה.
- צבע כתום: כל מקום שבו יש חפיפה בין הצבע האדום לצהוב, זו יבשה שיש לה נקודה אנטיפודית שגם היא נמצאת ביבשה.
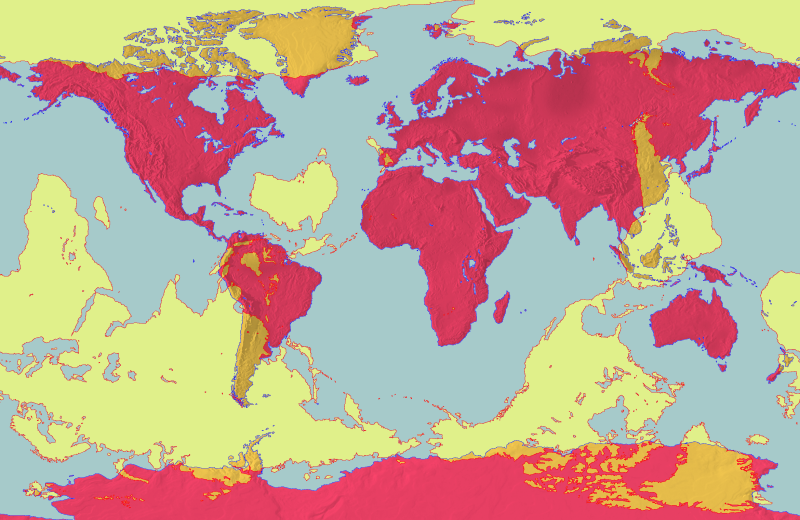
מקור: Johantheghost, CC BY-SA 3.0 http://creativecommons.org/licenses/by-sa/3.0/, via Wikimedia Commons
שטחי היבשה האנטיפודיים שמיד קופצים לעין אלו: צפון רוסיה, גרינלנד וצפון קנדה שכולם חופפים ליבשת אנטארקטיקה. שטח בולט נוסף נמצא במזרח סין עם מקבילה אנטיפודית בדרום אמריקה, במדינות ארגנטינה וצ'ילה. אמנם, חדי העין מביניכם כנראה שמו לב כי האי הצפוני של ניו-זילנד אנטיפודי לספרד. בתמונה הבאה תוכלו לראות זום-אין על האזור; ניתן לראות כי העיר וולינגטון בני-זילנד ומדריד בספרד נמצאות כמעט אחת מול השניה, משני צידי כדור הארץ:

מקור: Karte: NordNordWest, Lizenz: Creative Commons by-sa-3.0 de, CC BY-SA 3.0 DE https://creativecommons.org/licenses/by-sa/3.0/de/deed.en, via Wikimedia Commons
יש פה חור, אולי נקפוץ פנימה?
פיזיקאים שרואים תמונה כזו פשוט לא מסוגלים להחזיק את עצמם, ומיד לשאול את השאלה הסופר-דופר מתבקשת:
במידה ויכולנו לקדוח תעלה ישירות דרך מרכז כדור הארץ, כל הדרך ממדריד לוולינגטון, אז:
- מה יקרה אם נקפוץ לתוכה, למשל מהצד של ספרד?
- תוך כמה זמן נגיע לצד השני, אל ניו-זילנד, אם בכלל נגיע?
- באיזו מהירות נצא בצד השני?
לפני שנכנס לתוך מחילת הארנב – תרתי משמע – ראוי לציין נקודה נוספת: אלו מביניכם שאוהבים סרטי מדע בדיוני, בטח זוכרים כי הרעיון הנ"ל – תנועה דרך מרכז כדור הארץ – כבר הופיע בסרט "זיכרון גורלי" משנת 2012, שהיה עיבוד מחודש לסרט המקורי משנת 1990 בכיכובם של ארנולד שוורצנגר ושרון סטון. העלילה בסרט עוקבת אחר עובד מפעל ממורמר שנוסע לעבודה כל יום מצד אחד של כדור הארץ לצד השני, על ידי מעלית שעוברת ישירות דרך מרכז כדור הארץ.
בכנות, אני די סקפטי אם נצליח אי פעם לקדוח תעלה דרך מרכז כדור הארץ, הטמפרטורות שם פשוט גבוהות מדי. אבל אם תחזרו למאה ה-12 לספירה, ותנסו להסביר לריצ'רד לב-ארי מלך אנגליה כי בעתיד הוא יוכל לנסוע לבקר את פיליפ השני מלך צרפת דרך מנהרה מתחת לים, ישירות מהחוף הדרומי של אנגליה אל החוף הצפוני של צרפת, סביר להניח כי הוא היה ממנה אתכם לתפקיד ליצן החצר. אף על פי כן, עשינו זאת, והיום ניתן להגיע מאנגליה לצרפת ברכבת תת-ימית, מתחת למימי תעלת למנש. אז איך אומרים: Never say never.
כוח המשיכה בתוך כדור הארץ
אוקיי, אז נחזור לבעיה העיקרית שלנו:
החלטנו לקפוץ לתוך מנהרה אנכית, המחברת בין ספרד לניו-זילנד ישירות דרך מרכז כדור הארץ. מה יקרה?
די ברור שהמפתח לפתרון הבעיה תלוי בשאלה כיצד ישתנה כוח המשיכה, תוך כדי שאנו נופלים ומתקרבים למרכז כדור הארץ.2
ובכן, אייזק ניוטון בכבודו ובעצמו נדרש לבעיה הזו, והוכיח מתמטית, כי ככל שנרד פנימה אל תוך כדור הארץ, אנו נרגיש כוח משיכה קטן יותר ויותר, ביחס ישר למרחק שעוד נשאר לנו לעבור עד המרכז.3 במילים פשוטות:
- אם למשל ירדנו לעומק של חצי מהרדיוס – כלומר הגענו לנקודה הנמצאת בדיוק באמצע בין ספרד למרכז הכדור – באותה נקודה אנו נרגיש כוח משיכה הקטן פי שתיים מכוח המשיכה שהרגשנו על פני השטח.
- אם למשל עשינו 75% מהדרך אל המרכז, כך שנשאר לנו לעבור רק עוד רבע מאורכו הכולל של הרדיוס, באותה נקודה נרגיש כוח משיכה הקטן פי ארבע מכוח המשיכה על פני השטח.
- במרכז כדור הארץ לא נרגיש כוח משיכה כלל, כי "מיצינו" את כל אורכו של הרדיוס.
הצעד הבא בפתרון הבעיה הוא להבין כי קיימת סימטריה לאורך המסע שלנו מספרד לניו-זילנד. במילים אחרות: אין הבדל אם אנחנו נמצאים בין ספרד למרכז כדור הארץ, או בין מרכז כדור הארץ לניו-זילנד. בכל מקרה המשפט של ניוטון תקף: כוח המשיכה ישתנה אך ורק כתלות במרחק שלנו מן המרכז, וכיוון הכוח יהיה תמיד כלפי המרכז, לא משנה אם אנחנו נמצאים בצד של ספרד או בצד של ניו-זילנד.
כעת מגיע הפאנץ'-ליין: משני שיקולים אלו – אופן השינוי בכוח והסימטריה של הבעיה – נוכל להסיק כיצד הגוף במנהרה ינוע: אם פועל עליכם כוח כלפי המרכז וגודל הכוח עומד ביחס ישר למרחק מהמרכז, אז התנועה שתבצעו תהיה תנועה מחזורית סביב המרכז, מצד לצד, שוב ושוב, בדיוק כך:

מקור: Gotant6884, CC BY-SA 4.0 https://creativecommons.org/licenses/by-sa/4.0, via Wikimedia Commons
על ידי פתרון מלא של החוק השני של ניוטון, ניתן כמובן להוכיח מתמטית כי כוח עם תכונות שכאלה אכן יוצר תנועה מחזורית, כפי שציינתי לעיל. אך המטרה כאן היא לפשט רעיונות, ולא לסבך אותם; לכן במקום לפתור משוואות דיפרנציאליות, ניתן לראות כי הרציונל מאחורי המסקנה שלנו הוא די פשוט:
- לאחר שהתחלתם את הנפילה בספרד, כוח המשיכה ימשוך אתכם כלפי המרכז, ויגרום לכם לצבור מהירות.
- אמנם כוח המשיכה הולך ונחלש ככל שתתקרבו למרכז, אך הוא כל הזמן מכוון כלפי המרכז, ולכן הוא אינו יכול להאט אתכם.
- כשתגיעו למרכז כדור הארץ, כוח המשיכה יתבטל לגמרי אך זה לא אומר שאתם תעצרו. להיפך, אתם תחצו את המרכז במהירות שצברתם עד כה.
- מיד לאחר חציית המרכז, כוח המשיכה מתהפך ומיד מנסה להחזיר אתכם "אחורה", מה שיגרום לכם להאט והמהירות שלכם תלך ותקטן.
- דווקא בגלל הסימטריה של הבעיה, די ברור שהחצי של השני של המסע – מהמרכז לניו-זילנד – יהיה תמונת ראי של החצי הראשון! לכן אל ניו-זילנד נגיע בדיוק באותה מהירות שבה התחלנו בספרד; כלומר: בעצירה מוחלטת.
בשורה התחתונה: אתם תוכלו להיכנס למעלית – או לתוך קפסולה בתחילת המנהרה בצד הספרדי – לתת לקפסולה ליפול באופן חופשי, והקפסולה תעצור מעצמה בצד השני, בלי שאפילו תצטרכו ללחוץ על הבלמים. ברגע שהגעתם לניו-זילנד, כל מה שתצטרכו לעשות זה להרים את האמברקס, ולצאת החוצה.4
נו, מתי נגיע?
מה שבאמת מפתיע זו העובדה הבאה: כדי לחצות את כל כדור הארץ מקצה לקצה, לא לוקח כל כך הרבה זמן. אם אין לכם משהו יותר טוב לעשות, אתם מוזמנים לראות את החישוב המלא, שעשיתי עבורכם בקישור כאן. אך במידה ואתם קצרים בזמן פנוי, אתן לכם את התשובה הסופית:
42 דקות.
כן, זה הזמן שלוקח להגיע מספרד לניו-זילנד דרך מרכז כדור הארץ על ידי נפילה חופשית.5
אפילו פחות מהזמן שלוקח לי להגיע לעבודה בבוקר.
- דוגמה אחת לכך היא על פי הצל העגול שמטיל כדור הארץ על הירח בזמן ליקוי ירח [↩]
- לשם הפשטות נניח כי כדור הארץ עגול באופן מושלם עם צפיפות מסה אחידה. [↩]
- ההוכחה המתמטית של ניוטון נקראת: "משפט הקליפה", ובה הוא הוכיח שני טיעונים: 1. מחוץ לקליפה כדורית בעלת צפיפות מסה אחידה, כוח המשיכה מתנהג כאילו כל מסת הקליפה נמצאת בנקודה אחת במרכז הקליפה. 2. גוף הנמצא בתוך קליפה כדורית עם צפיפות מסה אחידה, אינו מרגיש כוח משיכה כלל, ללא תלות במיקום של הגוף בתוך הקליפה. משני טיעונים אלה ניתן להסיק כיצד כוח המשיכה פועל על גוף בתוך כדור הארץ. כיצד? את כדור הארץ ניתן לחלק לסדרה של קליפות כדוריות, אחת על גבי השנייה, כמו גלדי בצלים. עבור גוף שנמצא בתוך כדור הארץ, נקבל כי כל הקליפות שמעליו לא מפעילות עליו כוח משיכה, כי הגוף נמצא בתוכן. כל הקליפות שמתחתיו, מפעילות עליו כוח משיכה כאילו המסה של כולן נמצאת במרכז. כעת יש לזכור כי כוח המשיכה מכל הקליפות שמתחת לגוף נמצא ביחס הפוך למרחק הגוף מהמרכז בריבוע, אך המסה הכוללת של כל הקליפות שמתחת לגוף נמצאת ביחס ישר למרחק מהמרכז בשלישית. לכן התוצאה הסופית היא כי כוח המשיכה נמצא ביחס ישר למרחק מהמרכז, עד כדי מכפלה בקבוע פרופורציה. [↩]
- כמובן שלאורך כל הפוסט אנו מתעלמים מכוח החיכוך שיפעל על הקפסולה בזמן התנועה שלה. אם מוסיפים חיכוך לבעיה, כל העסק הופך להיות הרבה פחות משתלם; התנועה הופכת לאיטית יותר במידה מאוד משמעותית, ואין כלל אפשרות להגיע לצד השני ללא עזרה של הנעה פנימית. ראו למשל במאמר כאן: Gravity tunnel drag, arXiv:1606.01852 [↩]
- מסתבר כי אם לא מניחים צפיפות מסה אחידה של כדור הארץ, אלא לוקחים בחשבון את פרופיל צפיפות המסה המדודה של כדור הארץ, משך זמן התנועה מתקצר ל-38 דקות. ראו למשל במאמר כאן: The Gravity Tunnel in a Non-Uniform Earth, arXiv:1308.1342 [↩]


